题目内容
空间四边形ABCD中,AB=BC=CD=DA=BD=AC,E是AB的中点,若CE与平面BCD所成的角为θ,则( )
A、sinθ=
| ||||
B、sinθ=
| ||||
C、cosθ=
| ||||
D、cosθ=
|
考点:直线与平面所成的角
专题:空间位置关系与距离
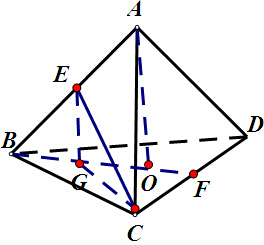
分析:由题意得到四面体为正四面体,分别过A、E作平面BCD的垂线,垂足分别是O、G,取CD的中点F,连接BF,CE,CG,CE与平面BCD所成的角∠ECG=θ,根据重心,求出直角三角形EGC的各边,计算即可.
解答:
解:分别过A、E作平面BCD的垂线,垂足分别是O、G,取CD的中点F,连接BF,CE,CG,
∴CE与平面BCD所成的角θ=∠ECG
令AB=1,
∵AB=BC=CD=DA=BD,
∴A-BCD是正四面体,
∴O为△BCD的重心,
∴BO=
BF,
∵△BCD是等边三角形,
∴BF=
CD=
,
∴BO=
×
=
,
∴AO=
=
=
,
∵AO⊥平面BCD、EG⊥平面BCD,
∴EG∥AO,又AE=BE,
∴EG=
AO=
,
显然有:CE=BF=
,
∴CE与平面BCD所成的角θ=∠ECG
∴sinθ=
=
.
故选:A
,
∴CE与平面BCD所成的角θ=∠ECG
令AB=1,
∵AB=BC=CD=DA=BD,
∴A-BCD是正四面体,
∴O为△BCD的重心,
∴BO=
| 2 |
| 3 |
∵△BCD是等边三角形,
∴BF=
| ||
| 2 |
| ||
| 2 |
∴BO=
| 2 |
| 3 |
| ||
| 2 |
| ||
| 3 |
∴AO=
| AB2-BO2 |
1-
|
| ||
| 3 |
∵AO⊥平面BCD、EG⊥平面BCD,
∴EG∥AO,又AE=BE,
∴EG=
| 1 |
| 2 |
| ||
| 6 |
显然有:CE=BF=
| ||
| 2 |
∴CE与平面BCD所成的角θ=∠ECG
∴sinθ=
| EG |
| CE |
| ||
| 2 |
故选:A
,

点评:本题主要考查了正四面体的性质,线面角的有关计算,作出线面角是关键,属于中档题.

练习册系列答案
相关题目
已知cos(θ+
)=-
,θ∈(0,
),则cos2θ等于( )
| π |
| 4 |
| ||
| 10 |
| π |
| 2 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
原点到直线3x+4y+5=0的距离为( )
| A、1 | B、2 | C、3 | D、4 |
设火箭发射成功的概率为0.99,若发射10次,其中失败的次数为X,则E(X)等于( )
| A、0.01 | ||
| B、9.9 | ||
| C、0.1 | ||
D、C
|
已知(5x-3)n的展开式中各项系数的和比(x-y-
)2n的展开式中各项系数的和多1023,则n的值为( )
| 1 |
| y |
| A、9 | B、10 | C、11 | D、12 |
若角α的终边在直线y=-2x上,且sina>0,则cosa值为( )
A、
| ||||
B、-
| ||||
C、-
| ||||
| D、-2 |
已知二面角α-l-β的大小为60°,异面直线m,n分别与α,β垂直,则m,n所成的角为( )
| A、120° | B、90° |
| C、60° | D、30° |
(
-
)n的展开式中只有第5项的二项式系数最大,则展开式中的常数项是( )
| 3 | x |
| 1 |
| x |
| A、28 | B、-28 |
| C、70 | D、-70 |