题目内容
函数f(x)=x3-ax-1=0在区间[2,+∞)内是增函数,则实数a的取值范围是 .
考点:利用导数研究函数的单调性
专题:导数的综合应用
分析:求函数的导数,根据函数的单调性和导数之间的关系即可得到结论.
解答:
解:若f(x)=x3-ax-1=0在区间[2,+∞)内是增函数,
则f′(x)=3x2-a≥0在区间[2,+∞)恒成立,
即a≤3x2,
∵3x2≥12,
∴a≤12,
故答案为:a≤12
则f′(x)=3x2-a≥0在区间[2,+∞)恒成立,
即a≤3x2,
∵3x2≥12,
∴a≤12,
故答案为:a≤12
点评:本题主要考查函数单调性和单调区间的应用,求函数的导数利用导数研究单调性是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
等比数列的前2项和为2,前4项和为10,则它的前6项和为( )
| A、31 | B、32 | C、41 | D、42 |
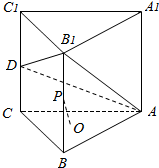 三棱柱ABC-A1B1C1中,点D、P为棱CC1、BB1的中点,O为△ABC重心,求证:OP∥平面AB1D.
三棱柱ABC-A1B1C1中,点D、P为棱CC1、BB1的中点,O为△ABC重心,求证:OP∥平面AB1D.