题目内容
已知sinα=
，α∈（
，π），则sin2α等于 ．
| 3 |
| 5 |
| π |
| 2 |
考点：二倍角的正弦
专题：三角函数的求值
分析：由条件利用同角三角函数的基本关系求得cosα的值，再利用二倍角的正弦公式求得sin2α的值．
解答：
解：∵sinα=
，α∈（
，π），∴cosα=-
=-
，
∴sin2α=2sinαcosα=2×
×（-
）=-
，
故答案为：-
．
| 3 |
| 5 |
| π |
| 2 |
| 1-sin2α |
| 4 |
| 5 |
∴sin2α=2sinαcosα=2×
| 3 |
| 5 |
| 4 |
| 5 |
| 24 |
| 25 |
故答案为：-
| 24 |
| 25 |
点评：本题主要考查同角三角函数的基本关系，二倍角公式的应用，属于基础题．
练习册系列答案
寒假大串联黄山书社系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
已知椭圆C：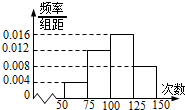
为了了解初中生的身体素质，某地区随机抽取了n名学生进行跳绳测试，根据所得数据画样本的频率分布直方图如图所示，且从左到右第一小组的频数是10，则n的值为设向量
=（2，t）与向量
=（1，3）共线，则t等于（ ）
| a |
| b |
| A、-6 | ||
B、
| ||
C、
| ||
| D、6 |