题目内容
已知函数f(x)=3x+x-5的零点x0∈[a,b],且b-a=1,a,b∈N*,则a+b=( )
| A、-2 | B、1 | C、2 | D、3 |
考点:函数的零点与方程根的关系
专题:函数的性质及应用
分析:由函数f(x)=3x+x-5,计算f(-1),f(0),f(-2),f(-1),f(1),f(2)的值;由根的存在性定理,求出f(x)的零点x0所在的区间.
解答:
解:∵函数f(x)=3x+x-5,
∴f(1)=31+1-5=-1<0,
f(2)=32+2-5=4=6>0,
∴f(1)f(2)<0;
∴f(x)的零点x0在区间(1,2)内.
∴a=1,b=2,
∴a+b=3,
故选:D.
∴f(1)=31+1-5=-1<0,
f(2)=32+2-5=4=6>0,
∴f(1)f(2)<0;
∴f(x)的零点x0在区间(1,2)内.
∴a=1,b=2,
∴a+b=3,
故选:D.
点评:本题考查了函数的零点的判定问题,解题时应用根的存在性定理,求出端点处的函数值,即可判定,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
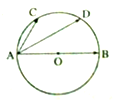
如图,已知AB是圆O的直径,点C,D等分
,已知
=
,
=
,则
等于( )
 |
| AB |
| AB |
| a |
| AC |
| b |
| AD |

A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
已知点P是双曲线
-
=1上一点,M,N是双曲线的左,右顶点,若直线PM的斜率的取值范围是[2,3],则直线PN的斜率的取值范围是( )
| x2 |
| 4 |
| y2 |
| 12 |
A、[1,
| ||||
B、[
| ||||
C、[
| ||||
D、[2,
|
执行如图所示的程序框图,则输出的a=( )


A、
| ||
B、-
| ||
| C、5 | ||
D、
|
边长为5,7,8的三角形的最大角与最小角的和是( )
| A、90° | B、150° |
| C、135° | D、120° |
已知“渐升数”是指每一位数字比其左边的数字大的正整数(如236),那么任取一个三位数,它是渐升数的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
将函数f(x)=sin(ωx+
)的图象关于x=
对称,则ω的值可能是( )
| π |
| 6 |
| π |
| 6 |
A、
| ||
B、
| ||
| C、5 | ||
| D、2 |
某几何体的三视图如图所示,则该几何体的表面积为( )


A、
| ||
B、
| ||
C、
| ||
D、
|