题目内容
 如图,已知R是实数集,集合A={x|log
如图,已知R是实数集,集合A={x|log| 1 |
| 2 |
| 2x-3 |
| x |
| A、[0,1] | ||
| B、[0,1) | ||
| C、(0,1) | ||
D、(1,
|
考点:Venn图表达集合的关系及运算
专题:集合
分析:阴影部分对应的集合为A∩B,利用集合的基本运算即可得到结论.
解答:
解:阴影部分对应的集合为A∩B,
∵A={x|log
(x-1)>0}={x|0<x-1<1}={x|1<x<2},
B={x|
<0}={x|x(2x-3)<0}={x|0<x<
},
∴A∩B={x|1<x<
},
故选:D
∵A={x|log
| 1 |
| 2 |
B={x|
| 2x-3 |
| x |
| 3 |
| 2 |
∴A∩B={x|1<x<
| 3 |
| 2 |
故选:D
点评:本题主要考查集合的基本运算,利用集合关系确定阴影部分的集合是解决本题的关键.

练习册系列答案
相关题目
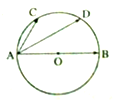
如图,已知AB是圆O的直径,点C,D等分
,已知
=
,
=
,则
等于( )
 |
| AB |
| AB |
| a |
| AC |
| b |
| AD |

A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
设M和N是两个集合,定义集合M-N=|x|x∈M,且x∉N|,如果M=|x|log2x<1|,N=|x|x-2<1|,那么M-N=( )
| A、{x|0<x<1} |
| B、{x|0<x≤1} |
| C、{x|1≤x<2} |
| D、{x|2≤x<3} |
已知i是虚数单位,则化简复数
的结果为( )
| -1+i |
| 1+i |
| A、i | B、-1 | C、-i | D、1 |
边长为5,7,8的三角形的最大角与最小角的和是( )
| A、90° | B、150° |
| C、135° | D、120° |
