题目内容
已知点A为圆C:x2+y2-4x-6y+12=0上的动点,另外一个动点P满足PA与圆C相切,且|PA|=
;直线y=kx+3与点P的轨迹相交于M,N两点,若|MN|≥2
,则实数k的取值范围是( )
| 3 |
| 3 |
A、[-
| ||||||||
B、[-
| ||||||||
C、[-
| ||||||||
D、[-
|
考点:直线与圆的位置关系
专题:直线与圆
分析:根据PA与圆C相切,且|PA|=
,由勾股定理可得|PC|=2,可得点P的轨迹方程为 (x-2)2+(y-3)2=4.再根据|MN|≥2
,由弦长公式可得可得点C到直线y=kx+3的距离小于或等于
=1,故有
≤1,由此求得k的范围.
| 3 |
| 3 |
22-(
|
| |2k-3+3| | ||
|
解答:
解:圆C:x2+y2-4x-6y+12=0 即 (x-2)2+(y-3)2=1,表示以C(2,3)为圆心、半径等于1的圆.
再根据PA与圆C相切,且|PA|=
,由勾股定理可得|PC|=2,故点P的轨迹方程为 (x-2)2+(y-3)2=4.
再根据|MN|≥2
,由弦长公式可得可得点C到直线y=kx+3的距离小于或等于
=1,
故有
≤1,求得-
≤k≤
,
故选:A.
再根据PA与圆C相切,且|PA|=
| 3 |
再根据|MN|≥2
| 3 |
22-(
|
故有
| |2k-3+3| | ||
|
| ||
| 3 |
| ||
| 3 |
故选:A.
点评:本题主要考查圆的标准方程,直线和圆相交的性质,点到直线的距离公式,弦长公式的应用,属于基础题.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
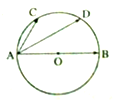
如图,已知AB是圆O的直径,点C,D等分
,已知
=
,
=
,则
等于( )
 |
| AB |
| AB |
| a |
| AC |
| b |
| AD |

A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
设M和N是两个集合,定义集合M-N=|x|x∈M,且x∉N|,如果M=|x|log2x<1|,N=|x|x-2<1|,那么M-N=( )
| A、{x|0<x<1} |
| B、{x|0<x≤1} |
| C、{x|1≤x<2} |
| D、{x|2≤x<3} |
已知i是虚数单位,则化简复数
的结果为( )
| -1+i |
| 1+i |
| A、i | B、-1 | C、-i | D、1 |
已知点P是双曲线
-
=1上一点,M,N是双曲线的左,右顶点,若直线PM的斜率的取值范围是[2,3],则直线PN的斜率的取值范围是( )
| x2 |
| 4 |
| y2 |
| 12 |
A、[1,
| ||||
B、[
| ||||
C、[
| ||||
D、[2,
|
将函数f(x)=sin(ωx+
)的图象关于x=
对称,则ω的值可能是( )
| π |
| 6 |
| π |
| 6 |
A、
| ||
B、
| ||
| C、5 | ||
| D、2 |
