题目内容
1. 如图,在正方体ABCD-A′B′C′D′中,M是AB上一点,N是A′C的中点,MN⊥平面A′DC,求证:MN∥AD′.
如图,在正方体ABCD-A′B′C′D′中,M是AB上一点,N是A′C的中点,MN⊥平面A′DC,求证:MN∥AD′.
分析 连接AC,BD,设交点为O,连接ON,OM,由MN⊥CD,NO⊥CD,可证CD⊥平面MNO,可证AB⊥OM,OM∥AD,又N在BD′上且为中点,从而可证MN∥AD′.
解答 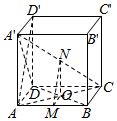 证明:连接AC,BD,设交点为O,连接ON,OM,
证明:连接AC,BD,设交点为O,连接ON,OM,
∵MN⊥平面A′DC,CD?平面A′DC
∴MN⊥CD,
∵在正方体ABCD-A′B′C′D′中,N是A1C的中点,O是AC的中点,
∴NO⊥CD,
∵MN∩NO=N,
∴CD⊥平面MNO,
∴CD⊥OM,CD∥AB
∴AB⊥OM,
∴OM∥AD,
又∵在正方体ABCD-A′B′C′D′中,N是A′C的中点,
∴N在BD′上,且为中点,
∴△AD′B中,MN∥AD′.
点评 本题主要考查了直线与平面垂直的性质,考查了空间想象能力和推理论证能力,作出恰当的辅助线是解题的关键,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11.以点(2,-2)为圆心并且与圆x2+y2+2x-4y+1=0相外切的圆的方程是( )
| A. | (x+2)2+(y+2)2=9 | B. | (x-2)2+(y+2)2=9 | C. | (x-2)2+(y-2)2=16 | D. | (x-2)2+(y+2)2=16 |
16.已知f(x)=sin(x+$\frac{π}{6}$),若sinα=$\frac{3}{5}$($\frac{π}{2}$<α<π),则f(α+$\frac{π}{12}$)=( )
| A. | $\frac{7\sqrt{2}}{10}$ | B. | -$\frac{\sqrt{2}}{10}$ | C. | $\frac{\sqrt{2}}{10}$ | D. | $\frac{7\sqrt{2}}{10}$ |
6.使函数f(x)=|x|与g(x)=-x2+2x都是增函数的区间可以是( )
| A. | [0,1] | B. | (-∞,1] | C. | (-∞,0] | D. | [0,2] |