题目内容
| ∫ |
0 |
考点:定积分
专题:导数的概念及应用
分析:求出被积函数的原函数,然后分别代入积分上限和积分下限后作差得答案.
解答:
解:∵(
sin4x)′=sin3xcosx,
∴
(sin3xcosx)dx=(
sin4x
=
sin4
-
sin40=
.
故答案为:
.
| 1 |
| 4 |
∴
| ∫ |
0 |
| 1 |
| 4 |
| )| |
0 |
| 1 |
| 4 |
| π |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
故答案为:
| 1 |
| 4 |
点评:本题考查了定积分,关键是求出被积函数的原函数,是基础题.

练习册系列答案
相关题目
设命题p:若|
|=|
|=
,且
与
的夹角是
,则向量
在
方向上的投影是1;命题q:“x≥1”是“
≤1”的充分不必要条件,下列判断正确的是( )
| a |
| b |
| 2 |
| a |
| b |
| 3π |
| 4 |
| b |
| a |
| 1 |
| x |
| A、p∨q是假命题 |
| B、p∧q是真命题 |
| C、p∨q是真命题 |
| D、﹁q为真命题 |
已知向量
=(3cosα,2)与向量
=(3,4sinα)平行,则锐角α等于( )
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知tanα=2
,且α∈(-π,0),则sinα-
cosα的值是( )
| 2 |
| 2 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
已知f(x)是定义在R上的奇函数,当x>0时,f(x)=log2x,则f(-8)值为( )
| A、3 | ||
B、
| ||
C、-
| ||
| D、-3 |
 某商场根据甲、乙两种不同品牌的洗衣粉在周一至周五每天的销量绘制成如图所示的茎叶图,则销量的中位数较大的品牌是
某商场根据甲、乙两种不同品牌的洗衣粉在周一至周五每天的销量绘制成如图所示的茎叶图,则销量的中位数较大的品牌是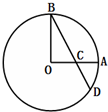 如图,A,B是圆O上两点,且OA⊥OB,OA=1,C为OA的中点,连接BC并延长交圆O于点D,则CD=
如图,A,B是圆O上两点,且OA⊥OB,OA=1,C为OA的中点,连接BC并延长交圆O于点D,则CD=