题目内容
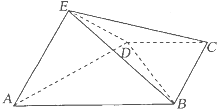 如图,在四棱锥E-ABCD中,平面EAD⊥平面ABCD,DC∥AB,BC⊥CD,EA⊥ED,AB=4,BC=CD=EA=ED=2,F是线段EB的中点.
如图,在四棱锥E-ABCD中,平面EAD⊥平面ABCD,DC∥AB,BC⊥CD,EA⊥ED,AB=4,BC=CD=EA=ED=2,F是线段EB的中点.(Ⅰ)证明:CF∥平面ADE;
(Ⅱ)证明:BD⊥AE.
考点:直线与平面平行的判定
专题:空间位置关系与距离
分析:(Ⅰ)取AE得中点G,连结FG,DG,将问题转化为证明四边形CFGD是平行四边形即可;
(Ⅱ)由数量关系可得BD⊥AD,从而由面面垂直的性质即得结论.
(Ⅱ)由数量关系可得BD⊥AD,从而由面面垂直的性质即得结论.
解答:
证明:(Ⅰ)取AE得中点G,连结FG,DG,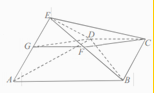
则有FG∥AB且FG=
AB=2,
又因为DC∥AB,CD=2,
所以FG∥DC,FG∥DC,
所以四边形CFGD是平行四边形.
所以CF∥GD,
又因为GD?平面ADE,CF?平面ADE,
所以CF∥平面ADE;
(Ⅱ)因为BC⊥CD,BC=CD=2,
所以BD=2
.
同理EA⊥ED,EA=ED=2,
所以AD=2
.
又因为AB=4,及勾股定理知BD⊥AD,
又因为平面EAD⊥平面ABCD,平面EAD∩平面ABCD=AD,BD?平面ABCD,
所以BD⊥平面EAD,
又因为AE?平面EAD,
所以BD⊥AE.

则有FG∥AB且FG=
| 1 |
| 2 |
又因为DC∥AB,CD=2,
所以FG∥DC,FG∥DC,
所以四边形CFGD是平行四边形.
所以CF∥GD,
又因为GD?平面ADE,CF?平面ADE,
所以CF∥平面ADE;
(Ⅱ)因为BC⊥CD,BC=CD=2,
所以BD=2
| 2 |
同理EA⊥ED,EA=ED=2,
所以AD=2
| 2 |
又因为AB=4,及勾股定理知BD⊥AD,
又因为平面EAD⊥平面ABCD,平面EAD∩平面ABCD=AD,BD?平面ABCD,
所以BD⊥平面EAD,
又因为AE?平面EAD,
所以BD⊥AE.
点评:本题考查线面垂直的判定及面面垂直的性质,作出恰当的辅助线、找到所给数据中隐含的条件是解决本题的关键,属中档题.

练习册系列答案
相关题目
已知实数2、t、8构成一个等比数列,则圆锥曲线
+y2=1的离心率为( )
| x2 |
| t |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
设命题p:若|
|=|
|=
,且
与
的夹角是
,则向量
在
方向上的投影是1;命题q:“x≥1”是“
≤1”的充分不必要条件,下列判断正确的是( )
| a |
| b |
| 2 |
| a |
| b |
| 3π |
| 4 |
| b |
| a |
| 1 |
| x |
| A、p∨q是假命题 |
| B、p∧q是真命题 |
| C、p∨q是真命题 |
| D、﹁q为真命题 |
已知tanα=2
,且α∈(-π,0),则sinα-
cosα的值是( )
| 2 |
| 2 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
 某商场根据甲、乙两种不同品牌的洗衣粉在周一至周五每天的销量绘制成如图所示的茎叶图,则销量的中位数较大的品牌是
某商场根据甲、乙两种不同品牌的洗衣粉在周一至周五每天的销量绘制成如图所示的茎叶图,则销量的中位数较大的品牌是