题目内容
6.已知x∈R,下列不等式中正确的是( )| A. | $\frac{1}{{2}^{x}}$>$\frac{1}{{3}^{x}}$ | B. | $\frac{1}{{x}^{2}-x+1}$>$\frac{1}{{x}^{2}+x+1}$ | ||
| C. | $\frac{1}{{x}^{2}+1}$>$\frac{1}{{x}^{2}+2}$ | D. | $\frac{1}{2|x|}$>$\frac{1}{{x}^{2}+1}$ |
分析 举反例可排除A、B、D,再证明C正确即可.
解答 解:取x=0可得$\frac{1}{{2}^{x}}$=1=$\frac{1}{{3}^{x}}$,故A错误;
取x=0可得$\frac{1}{{x}^{2}-x+1}$=1=$\frac{1}{{x}^{2}+x+1}$,故B错误;
取x=1可得$\frac{1}{2|x|}$=$\frac{1}{2}$=$\frac{1}{{x}^{2}+1}$,故D错误;
选项C,∵x2+2>x2+1>0,∴$\frac{1}{{x}^{2}+1}$>$\frac{1}{{x}^{2}+2}$,故正确.
故选:C
点评 本题考查不等式比较大小,举反例是解决问题的关键,属基础题.

练习册系列答案
相关题目
14.函数y=cos(2x-$\frac{π}{2}$)是( )
| A. | 最小正周期为2π的偶函数 | B. | 最小正周期为π的偶函数 | ||
| C. | 最小正周期为2π的奇函数 | D. | 最小正周期为π的奇函数 |
15.设$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$,$\overrightarrow{{e}_{3}}$是不共面的三个单位向量,则下列向量组不能作为空间的一个基底的一组是( )
| A. | {$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$,$\frac{1}{2}$$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{3}}$,$\overrightarrow{{e}_{2}}$+2$\overrightarrow{{e}_{3}}$} | B. | {$\overrightarrow{{e}_{1}}$-$\overrightarrow{{e}_{3}}$,$\overrightarrow{{e}_{2}}$+$\overrightarrow{{e}_{3}}$,$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$} | ||
| C. | {$\overrightarrow{{e}_{1}}$-$\overrightarrow{{e}_{2}}$,$\overrightarrow{{e}_{2}}$-2$\overrightarrow{{e}_{3}}$,$\overrightarrow{{e}_{3}}$-3$\overrightarrow{{e}_{1}}$} | D. | {$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{3}}$,$\overrightarrow{{e}_{2}}$+$\overrightarrow{{e}_{3}}$,$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$} |
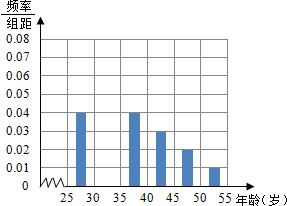 某班同学参加社会实践活动,本市25~55岁年龄段的人群进行某项随机调查,得到各年龄段被调查人数的频率分布直方图如下(部分缺损)
某班同学参加社会实践活动,本市25~55岁年龄段的人群进行某项随机调查,得到各年龄段被调查人数的频率分布直方图如下(部分缺损)