题目内容
11.设集合A={x|a<x<a+2},B={x|1<x<2},且A∪∁RB=R,则实数a的取值范围是[0,1].分析 求出集合B的补集,求和列出不等式组求解即可.
解答 解:集合A={x|a<x<a+2},B={x|1<x<2},∁RB={x|x≤1或x≥2},
A∪∁RB=R,
可得$\left\{\begin{array}{l}a≤1\\ a+2≥2\end{array}\right.$,
解得a∈[0,1].
故答案为:[0,1].
点评 本题考查转化思想的应用,集合的基本运算,是基础题.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
2.设f(x)=$\frac{1+x}{1-x}$,又记f1(x)=f(x),fk+1(x)=f(fk(x)),k=1,2,…,则f2008(x)=( )
| A. | $\frac{1+x}{1-x}$ | B. | $\frac{x-1}{x+1}$ | C. | x | D. | -$\frac{1}{x}$ |
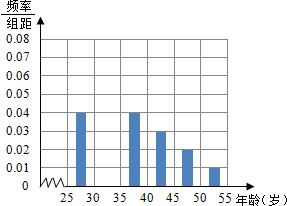 某班同学参加社会实践活动,本市25~55岁年龄段的人群进行某项随机调查,得到各年龄段被调查人数的频率分布直方图如下(部分缺损)
某班同学参加社会实践活动,本市25~55岁年龄段的人群进行某项随机调查,得到各年龄段被调查人数的频率分布直方图如下(部分缺损)