题目内容
10.P、Q分别为3x+4y-12=0与6x+8y+1=0上任一点,则|PQ|的最小值为( )| A. | $\frac{13}{5}$ | B. | 3 | C. | $\frac{5}{2}$ | D. | 6 |
分析 直接利用平行线之间的距离公式求解即可.
解答 解:P、Q分别为3x+4y-12=0与6x+8y+1=0上任一点,则|PQ|的最小值就是平行线之间的距离,
所以最小值为:$\frac{|\frac{1}{2}+12|}{\sqrt{{3}^{2}+{4}^{2}}}$=$\frac{\frac{25}{2}}{5}$=$\frac{5}{2}$.
故选:C.
点评 本题考查平行线之间的距离公式的应用,转化思想的应用,考查计算能力.

练习册系列答案
相关题目
20.已知sin(α+π)=$\frac{1}{2}$,且$α∈(-\frac{π}{2},0)$,则tanα的值为( )
| A. | $-\frac{{\sqrt{3}}}{3}$ | B. | $\sqrt{3}$ | C. | $-\frac{1}{2}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
15.设$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$,$\overrightarrow{{e}_{3}}$是不共面的三个单位向量,则下列向量组不能作为空间的一个基底的一组是( )
| A. | {$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$,$\frac{1}{2}$$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{3}}$,$\overrightarrow{{e}_{2}}$+2$\overrightarrow{{e}_{3}}$} | B. | {$\overrightarrow{{e}_{1}}$-$\overrightarrow{{e}_{3}}$,$\overrightarrow{{e}_{2}}$+$\overrightarrow{{e}_{3}}$,$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$} | ||
| C. | {$\overrightarrow{{e}_{1}}$-$\overrightarrow{{e}_{2}}$,$\overrightarrow{{e}_{2}}$-2$\overrightarrow{{e}_{3}}$,$\overrightarrow{{e}_{3}}$-3$\overrightarrow{{e}_{1}}$} | D. | {$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{3}}$,$\overrightarrow{{e}_{2}}$+$\overrightarrow{{e}_{3}}$,$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$} |
2.设f(x)=$\frac{1+x}{1-x}$,又记f1(x)=f(x),fk+1(x)=f(fk(x)),k=1,2,…,则f2008(x)=( )
| A. | $\frac{1+x}{1-x}$ | B. | $\frac{x-1}{x+1}$ | C. | x | D. | -$\frac{1}{x}$ |
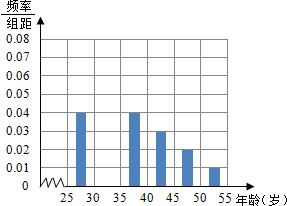 某班同学参加社会实践活动,本市25~55岁年龄段的人群进行某项随机调查,得到各年龄段被调查人数的频率分布直方图如下(部分缺损)
某班同学参加社会实践活动,本市25~55岁年龄段的人群进行某项随机调查,得到各年龄段被调查人数的频率分布直方图如下(部分缺损) (3)请认真阅读下列程序框图:已知程序框图
(3)请认真阅读下列程序框图:已知程序框图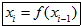 中的函数关系式为$f(x)=\frac{4x-2}{x+1}$,程序框图中的D为函数f(x)的定义域,把此程序框图中所输出的数xi组成一个数列{xn}
中的函数关系式为$f(x)=\frac{4x-2}{x+1}$,程序框图中的D为函数f(x)的定义域,把此程序框图中所输出的数xi组成一个数列{xn}