题目内容
12.圆(x-3)2+(y-3)2=9上到直线3x+4y-11=0的距离等于2的点有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 确定圆心和半径,求出圆心到直线的距离,与半径比较,数形结合可知共有三个交点.
解答  解:(x-3)2+(y-3)2=9是一个以(3,3)为圆心,3为半径的圆.
解:(x-3)2+(y-3)2=9是一个以(3,3)为圆心,3为半径的圆.
圆心到3x+4y-11=0的距离为d=$\frac{|3×3+4×3-11|}{5}$=2,即AD=2,
∴ED=1,即圆周上E到已知直线的距离为1,
∴圆上的点到直线3x+4y-11=0的距离为2的点有2个.
故选:B.
点评 本题考查了直线与圆的位置关系,用到点到直线的距离公式,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
20.已知sin(α+π)=$\frac{1}{2}$,且$α∈(-\frac{π}{2},0)$,则tanα的值为( )
| A. | $-\frac{{\sqrt{3}}}{3}$ | B. | $\sqrt{3}$ | C. | $-\frac{1}{2}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
2.设f(x)=$\frac{1+x}{1-x}$,又记f1(x)=f(x),fk+1(x)=f(fk(x)),k=1,2,…,则f2008(x)=( )
| A. | $\frac{1+x}{1-x}$ | B. | $\frac{x-1}{x+1}$ | C. | x | D. | -$\frac{1}{x}$ |
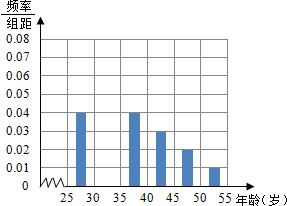 某班同学参加社会实践活动,本市25~55岁年龄段的人群进行某项随机调查,得到各年龄段被调查人数的频率分布直方图如下(部分缺损)
某班同学参加社会实践活动,本市25~55岁年龄段的人群进行某项随机调查,得到各年龄段被调查人数的频率分布直方图如下(部分缺损)