题目内容
设F为双曲线C：
-
=1（a＞0，b＞0）的右焦点，过点F且斜率为-1的直线l与双曲线C的两条渐近线分别交于A，B两点，若
=-3
，则双曲线C的离心率e=（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| AB |
| AF |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点：双曲线的简单性质
专题：计算题,平面向量及应用,圆锥曲线的定义、性质与方程
分析：设出过焦点的直线方程，与双曲线的渐近线方程联立把A，B表示出来，再由
=-3
，求出a，b，c，然后求双曲线的离心率．
| AB |
| AF |
解答：
解：设F（c，0），则过双曲线：
-
=1（a＞0，b＞0）的右焦点F
作斜率为-1的直线为：y=-（x-c），
而渐近线的方程是：y=±
x，
由
得：B（
，-
），
由
得，A（
，
），
=（
，-
），
=（
，-
），
由
=-3
，则
=-3•
，
即有b=
a，则c=
=
a，
则e=
=
．
故选D．
| x2 |
| a2 |
| y2 |
| b2 |
作斜率为-1的直线为：y=-（x-c），
而渐近线的方程是：y=±
| b |
| a |
由
|
| ac |
| a-b |
| bc |
| a-b |
由
|
| ac |
| a+b |
| bc |
| a+b |
| AB |
| 2abc |
| a2-b2 |
| 2abc |
| a2-b2 |
| AF |
| bc |
| a+b |
| bc |
| a+b |
由
| AB |
| AF |
| 2abc |
| a2-b2 |
| bc |
| a+b |
即有b=
| 5 |
| 3 |
| a2+b2 |
| ||
| 3 |
则e=
| c |
| a |
| ||
| 3 |
故选D．
点评：本题考查双曲线的性质和应用，解题时要认真审题，仔细解答，注意向量共线的合理运用．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知集合A={x|y=
，B={y|y=
，则A∩B=（ ）
| 1-x |
| 1-x |
| A、{1} | B、R |
| C、{-∞，1} | D、[0.1] |
已知命题p：2＜x＜3，q：x2-5x+4＜0，则p是q的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
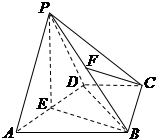如图，在四棱锥P-ABCD中，侧面PAD是等边三角形，AB∥CD，AB=2CD，BC⊥CD，∠DBC=30°，点E，F分别为AD，PB的中点．
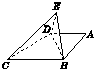如图，在直角梯形ABCD中，AD∥BC，AD=AB，∠A=90°，BD⊥DC，将△ABD沿BD折起到△EBD的位置，使平面EBD⊥平面BDC．
