一个高为1的正三棱锥的底面正三角形的边长为6.则此三棱锥的侧面积为18．题目和参考答案——青夏教育精英家教网—

题目内容

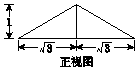
16．一个高为1的正三棱锥的底面正三角形的边长为6，则此三棱锥的侧面积为18．

分析画出满足题意的三棱锥P-ABC图形，根据题意，作出高，利用直角三角形，求出此三棱锥的侧面上的高，即可求出棱锥的侧面积．

解答解：由题意作出图形如图：
因为三棱锥P-ABC是正三棱锥，顶点在底面上的射影D是底面的中心，
在三角PDF中，
∵三角形PDF三边长PD=1，DF=$\sqrt{3}$，
∴PF=2
则这个棱锥的侧面积S_侧=3×$\frac{1}{2}$×6×1=18．
故答案为：18．

点评本题考查棱柱、棱锥、棱台的侧面积和表面积，棱锥的结构特征，还考查计算能力，是基础题．

练习册系列答案

150加50篇英语完形填空与阅读理解系列答案

相关题目

6．已知命题p：?x₀∈[1，2]，x₀²-4x₀+6＜0，则￢p为（　　）

	A．	?x∉[1，2]，x²-4x+6≥0		B．	?x₀∈[1，2]，x₀²-4x₀+6≥0
	C．	?x∉[1，2]，x²-4x+6＞0		D．	?x∈[1，2]，x²-4x+6≥0

7．数列{a_n}的通项公式为${a_n}={n^2}+kn$，那么k≥-2是{a_n}为递增数列的（　　）

	A．	充分不必要条件		B．	必要不充分条件
	C．	充要条件		D．	既不充分也不必要条件

4．函数y=e${\;}^{-{x}^{2}+2x}$（0≤x＜3）的值域是（　　）

11．在平行四边形ABCD中，AB=3，AD=4，则$\overrightarrow{AC}$•（$\overrightarrow{AB}$-$\overrightarrow{AD}$）等于（　　）

1．已知函数f（x）=2sinxcosx+2$\sqrt{3}$cos2x-$\sqrt{3}$．
（1）求函数f（x）的单调减区间；
（2）已知△ABC中角A，B，C所对的边分别是a，b，c，其中b=2，若锐角A满足f（$\frac{A}{2}$-$\frac{π}{6}$）=3，且$\frac{π}{4}$≤B≤$\frac{π}{3}$，求边c的取值范围．

8．已知三棱锥的四个面都是腰长为2的等腰三角形，该三棱锥的正视图如图所示，则该三棱锥的体积是$\frac{\sqrt{3}}{3}$

5．已知2sin（π-x）+1=0，则cos2x=$\frac{1}{2}$．

6．已知点P是△ABC所在平面内一点，且$\overrightarrow{PA}$=-2$\overrightarrow{PB}$，在△ABC内任取一点Q，则Q落在△APC内的概率为（　　）

试题分类