题目内容
1.已知函数f(x)=2sinxcosx+2$\sqrt{3}$cos2x-$\sqrt{3}$.(1)求函数f(x)的单调减区间;
(2)已知△ABC中角A,B,C所对的边分别是a,b,c,其中b=2,若锐角A满足f($\frac{A}{2}$-$\frac{π}{6}$)=3,且$\frac{π}{4}$≤B≤$\frac{π}{3}$,求边c的取值范围.
分析 (1)利用倍角公式、和差公式可化简f(x),再利用正弦函数的单调性即可得出.
(2)由$f(\frac{A}{2}-\frac{π}{6})=\sqrt{3}$且角A为锐角得:$A=\frac{π}{3}$.又由正弦定理$\frac{b}{sinB}=\frac{c}{sinC}$及b=2,可得c.
解答 解:(1)∵$f(x)=2sinxcosx+2\sqrt{3}{cos^2}x-\sqrt{3}$,∴$f(x)=sin2x+\sqrt{3}cos2x=2sin(2x+\frac{π}{3})$(3分)∴$当2kπ+\frac{π}{2}≤2x+\frac{π}{3}≤\frac{3π}{2}+2kπ,k∈Z时,解得$$kπ+\frac{π}{12}≤x≤\frac{7π}{12}+kπ,k∈Z$(6分)
因此,函数f(x)的单调减区间为$[kπ+\frac{π}{12},\frac{7π}{12}+kπ](k∈Z)$(7分)
(2)由$f(\frac{A}{2}-\frac{π}{6})=\sqrt{3}$且角A为锐角得:$A=\frac{π}{3}$ (9分)
又由正弦定理$\frac{b}{sinB}=\frac{c}{sinC}$及b=2,
∴$c=\frac{2sinC}{sinB}=\frac{2sin(A+B)}{sinB}=\frac{{sinB+\sqrt{3}cosB}}{sinB}=1+\frac{{\sqrt{3}}}{tanB}$(2分)
∵$\frac{π}{4}≤B≤\frac{π}{3}$,∴$2≤c≤1+\sqrt{3}$(14分)
点评 本题考查了倍角公式、和差公式、正弦函数的单调性、正弦定理、三角函数求值,考查了推理能力与计算能力,属于中档题.

 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案| A. | $\sqrt{2}f(-\frac{π}{3})<f(\frac{π}{4})$ | B. | $\sqrt{2}f(-\frac{π}{3})<f(-\frac{π}{4})$ | C. | $f(0)>\sqrt{2}f(-\frac{π}{4})$ | D. | $f(\frac{π}{6})<\sqrt{3}f(\frac{π}{3})$ |
| A. | 向左平移$\frac{π}{6}$个单位长度 | B. | 向右平移$\frac{π}{6}$个单位长度 | ||
| C. | 向左平移$\frac{π}{12}$个单位长度 | D. | 向右平移$\frac{π}{12}$个单位长度 |
| A. | 25 | B. | 16 | C. | 9 | D. | 4 |
 如图,已知△ABC中,D为边BC上靠近B点的三等分点,连接AD,E为线段AD的中点,若$\overrightarrow{CE}=m\overrightarrow{AB}+n\overrightarrow{AC}$,则m+n=$-\frac{1}{2}$.
如图,已知△ABC中,D为边BC上靠近B点的三等分点,连接AD,E为线段AD的中点,若$\overrightarrow{CE}=m\overrightarrow{AB}+n\overrightarrow{AC}$,则m+n=$-\frac{1}{2}$.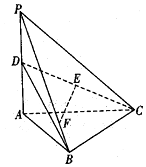 如图,三棱锥P-ABC中,PA⊥平面ABC,∠ABC=90°,PA=AC=2,D是PA的中点,E是CD的中点,点F在PB上,$\overrightarrow{PF}=3\overrightarrow{FB}$.
如图,三棱锥P-ABC中,PA⊥平面ABC,∠ABC=90°,PA=AC=2,D是PA的中点,E是CD的中点,点F在PB上,$\overrightarrow{PF}=3\overrightarrow{FB}$.