题目内容
5．已知2sin（π-x）+1=0，则cos2x=$\frac{1}{2}$．分析 已知等式利用诱导公式化简求出sinx的值，原式利用二倍角的余弦函数公式化简，将sinx的值代入计算即可求出值．
解答 解：已知等式整理得：2sinx+1=0，
解得：sinx=-$\frac{1}{2}$，
则原式=1-2sin2x=1-2×$\frac{1}{4}$=$\frac{1}{2}$，
故答案为：$\frac{1}{2}$．
点评 此题考查了运用诱导公式化简求值，以及二倍角的余弦函数公式，熟练掌握公式是解本题的关键．
练习册系列答案
活力课时同步练习册系列答案
相关题目
15．已知A+B=$\frac{π}{3}$，则tanA+tanB+$\sqrt{3}$tanAtanB-$\sqrt{3}$的值等于（ ）
| A． | -2$\sqrt{3}$ | B． | 2$\sqrt{3}$ | C． | 0 | D． | 1-$\sqrt{3}$ |
13．已知数列{bn}是等比数列，b9是3和5等差中项，则b1b17=（ ）
| A． | 25 | B． | 16 | C． | 9 | D． | 4 |
17．
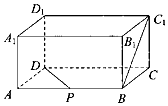如图，在长方体ABCD-A1B1C1D1中，AB=2，BC=1，BB1=1，P是AB的中点，则异面直线BC1与PD所成角等于（ ）
如图，在长方体ABCD-A1B1C1D1中，AB=2，BC=1，BB1=1，P是AB的中点，则异面直线BC1与PD所成角等于（ ）| A． | 30° | B． | 45° | C． | 60° | D． | 90° |