题目内容
4.函数y=e${\;}^{-{x}^{2}+2x}$(0≤x<3)的值域是( )| A. | (0,1] | B. | (e-3,e] | C. | [e-3,1] | D. | [1,e] |
分析 先求出0≤x<3时-x2+2x的取值范围,再根据指数函数的单调性求出值域.
解答 解:∵y=e${\;}^{-{x}^{2}+2x}$=e${\;}^{-(x-1)^{2}+1}$(0≤x<3),
当0≤x<3时,-3<-(x-1)2+1≤1,
∴e-3<e${\;}^{-(x-1)^{2}+1}$≤e1,
即e-3<y≤e;
∴函数y的值域是(e-3,e].
故选:B.
点评 本题考查了求复合函数的值域问题,解题时应考查复合函数的单调性,从而求出函数的值域,是基础题.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
14.已知向量$\overrightarrow{a}$=(2,1),$\overrightarrow{b}$=(1,x),若$\overrightarrow{a}$+$\overrightarrow{b}$与$2\overrightarrow a-\overrightarrow b$平行,则实数x的值是( )
| A. | -2 | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
15.已知A+B=$\frac{π}{3}$,则tanA+tanB+$\sqrt{3}$tanAtanB-$\sqrt{3}$的值等于( )
| A. | -2$\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 0 | D. | 1-$\sqrt{3}$ |
9.已知偶函数y=f(x)对于任意的$x∈[0,\frac{π}{2})$满足f'(x)cosx+f(x)sinx>0(其中f'(x)是函数f(x)的导函数),则下列不等式中成立的是( )
| A. | $\sqrt{2}f(-\frac{π}{3})<f(\frac{π}{4})$ | B. | $\sqrt{2}f(-\frac{π}{3})<f(-\frac{π}{4})$ | C. | $f(0)>\sqrt{2}f(-\frac{π}{4})$ | D. | $f(\frac{π}{6})<\sqrt{3}f(\frac{π}{3})$ |
13.已知数列{bn}是等比数列,b9是3和5等差中项,则b1b17=( )
| A. | 25 | B. | 16 | C. | 9 | D. | 4 |
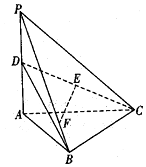 如图,三棱锥P-ABC中,PA⊥平面ABC,∠ABC=90°,PA=AC=2,D是PA的中点,E是CD的中点,点F在PB上,$\overrightarrow{PF}=3\overrightarrow{FB}$.
如图,三棱锥P-ABC中,PA⊥平面ABC,∠ABC=90°,PA=AC=2,D是PA的中点,E是CD的中点,点F在PB上,$\overrightarrow{PF}=3\overrightarrow{FB}$.