题目内容
8.已知三棱锥的四个面都是腰长为2的等腰三角形,该三棱锥的正视图如图所示,则该三棱锥的体积是$\frac{\sqrt{3}}{3}$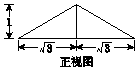
分析 先求出三棱锥高为h=1,由此能求出该三棱锥的体积.
解答 解:∵三棱锥每个面都是腰为2的等腰三角形,∴由正视图可得如下俯视图,
且三棱锥高为h=1,
则该三棱锥的体积V=$\frac{1}{3}sh$=$\frac{1}{3}×(\frac{1}{2}×2\sqrt{3}×1)×1$=$\frac{\sqrt{3}}{3}$.
故答案为:$\frac{\sqrt{3}}{3}$.
点评 本题考查三棱锥的体积的求法,是中档题,解题时要认真审题,注意三棱锥的性质的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.已知数列{an}中;a1=3,a2=6,且an+2=an+1-an,则数列的第100项为( )
| A. | 3 | B. | -3 | C. | 6 | D. | -6 |
13.已知数列{bn}是等比数列,b9是3和5等差中项,则b1b17=( )
| A. | 25 | B. | 16 | C. | 9 | D. | 4 |
17.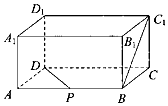 如图,在长方体ABCD-A1B1C1D1中,AB=2,BC=1,BB1=1,P是AB的中点,则异面直线BC1与PD所成角等于( )
如图,在长方体ABCD-A1B1C1D1中,AB=2,BC=1,BB1=1,P是AB的中点,则异面直线BC1与PD所成角等于( )
 如图,在长方体ABCD-A1B1C1D1中,AB=2,BC=1,BB1=1,P是AB的中点,则异面直线BC1与PD所成角等于( )
如图,在长方体ABCD-A1B1C1D1中,AB=2,BC=1,BB1=1,P是AB的中点,则异面直线BC1与PD所成角等于( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |