题目内容
7.数列{an}的通项公式为${a_n}={n^2}+kn$,那么k≥-2是{an}为递增数列的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
分析 由{an}为递增数列?an+1>an,解出即可判断出结论.
解答 解:由an+1>an,(n+1)2+k(n+1)>n2+kn,化为:k>-(2n+1),
由{an}为递增数列,可得k>-3.
∴k≥-2是{an}为递增数列的充分不必要条件.
故选:A.
点评 本题考查了不等式的解法、数列的单调性、简易逻辑的判定方法,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
18.已知数列{an}中;a1=3,a2=6,且an+2=an+1-an,则数列的第100项为( )
| A. | 3 | B. | -3 | C. | 6 | D. | -6 |
15.已知A+B=$\frac{π}{3}$,则tanA+tanB+$\sqrt{3}$tanAtanB-$\sqrt{3}$的值等于( )
| A. | -2$\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 0 | D. | 1-$\sqrt{3}$ |
17.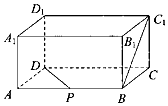 如图,在长方体ABCD-A1B1C1D1中,AB=2,BC=1,BB1=1,P是AB的中点,则异面直线BC1与PD所成角等于( )
如图,在长方体ABCD-A1B1C1D1中,AB=2,BC=1,BB1=1,P是AB的中点,则异面直线BC1与PD所成角等于( )
 如图,在长方体ABCD-A1B1C1D1中,AB=2,BC=1,BB1=1,P是AB的中点,则异面直线BC1与PD所成角等于( )
如图,在长方体ABCD-A1B1C1D1中,AB=2,BC=1,BB1=1,P是AB的中点,则异面直线BC1与PD所成角等于( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
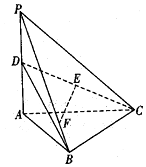 如图,三棱锥P-ABC中,PA⊥平面ABC,∠ABC=90°,PA=AC=2,D是PA的中点,E是CD的中点,点F在PB上,$\overrightarrow{PF}=3\overrightarrow{FB}$.
如图,三棱锥P-ABC中,PA⊥平面ABC,∠ABC=90°,PA=AC=2,D是PA的中点,E是CD的中点,点F在PB上,$\overrightarrow{PF}=3\overrightarrow{FB}$.