题目内容
16．
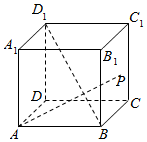如图，正方体ABCD-A1B1C1D1中，点P在侧面BCC1B1及其边界上运动，并且总是保持AP⊥BD1，试证明动点P在线段B1C上．
分析 连接AC，BD，利用正方体的性质以及线面垂直的性质定理，结合点在平面内的判定方法证明．
解答 
证明：连接AC，BD，∵AC⊥BD
∴AC⊥BD1，
连接AB1，A1B，∵AB1⊥A1B，∴A1B⊥BD1，∴BD1⊥平面AB1C，∴AP⊥BD1，A∈平面AB1C，
∴P∈平面AB1C，∵P∈平面BCC1B1，
又平面AB1C∩平面BCC1B1，∴P在线段B1C上．
点评 本题考查了空间线面垂直以及点与面关系的判定；关键是判定出P在两个平面内，从而在两个面的交线上．
练习册系列答案
名校练考卷期末冲刺卷系列答案
相关题目
7．函数f（x）=tan（2x+$\frac{π}{3}$），则（ ）
| A． | 函数最小正周期为π，且在（-$\frac{5π}{12}$，$\frac{π}{12}$）是增函数 | |
| B． | 函数最小正周期为$\frac{π}{2}$，且在（-$\frac{5π}{12}$，$\frac{π}{12}$）是减函数 | |
| C． | 函数最小正周期为π，且在（$\frac{π}{12}$，$\frac{7π}{12}$）是减函数 | |
| D． | 函数最小正周期为$\frac{π}{2}$，且在（$\frac{π}{12}$，$\frac{7π}{12}$）是增函数 |
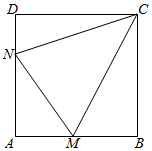如图所示，某村积极开展“美丽乡村•生态家园”建设，现拟在边长为1千米的正方形地块ABCD上划出一片三角形地块CMN建设美丽乡村生态公园，给村民休闲健身提供去处．点M，N分别在边AB，AD上．