题目内容
1.已知等差数列{an}满足a1+a2=10,a4-a3=2.(1)求数列{an}的通项公式;
(2)若等比数列{bn}满足b2=a3,b3=a7,求数列{bn}的通项公式.
分析 (1)设出等差数列的公差,由已知列式求得公差,进一步求出首项,代入等差数列的通项公式求数列{an}的通项公式;
(2)由b2=a3,b3=a7,结合(1)中等差数列的通项公式求得b2,b3的值,进一步求得等比数列的公比q及首项,则等比数列的通项公式可求.
解答 解:(1)设等差数列{an}的公差为d,则d=a4-a3=2,
又a1+a2=10,
∴2a1+d=10,解得a1=4,
∴an=4+2(n-1)=2n+2;
(2)设等比数列{bn}的公比为q,
由(1)知b2=a3=8,b3=a7=16,
∴$q=\frac{{b}_{3}}{{b}_{2}}=2$,
又b2=8=b1q,有b1=4,
∴${b}_{n}=4×{2}^{n-1}={2}^{n+1}$.
点评 本题考查数列递推式,考查了等差数列与等比数列通项公式的求法,是基础题.

练习册系列答案
相关题目
11.在△ABC中,角A、B、C的对边分别为a、b、c,若cos2A+cos2C+$\sqrt{2}$sinAsinC=1+cos2B.则$\sqrt{2}$sinA+cosC的最大值是( )
| A. | 1 | B. | 2 | C. | $\frac{3\sqrt{2}}{2}$ | D. | $\sqrt{5}$ |
6.已知为虚数单位,复数z满足z=$\frac{1+i}{1-i}$,则z2=( )
| A. | 1 | B. | -1 | C. | 2i | D. | -2i |
13.复数z=$\frac{(1-i)^{2}}{3+i}$的所对应的点位于复平面的( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
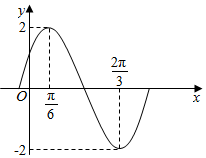 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)(x∈R)的部分图象如图所示.(Ⅰ)求函数f(x)的解析式并求函数f(x)的单调递增区间;
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)(x∈R)的部分图象如图所示.(Ⅰ)求函数f(x)的解析式并求函数f(x)的单调递增区间;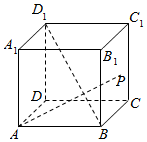 如图,正方体ABCD-A1B1C1D1中,点P在侧面BCC1B1及其边界上运动,并且总是保持AP⊥BD1,试证明动点P在线段B1C上.
如图,正方体ABCD-A1B1C1D1中,点P在侧面BCC1B1及其边界上运动,并且总是保持AP⊥BD1,试证明动点P在线段B1C上.