题目内容
6.已知(x+$\frac{m}{x}$)n展开式的二项式系数之和为256(1)求n;
(2)若展开式中常数项为$\frac{35}{8}$,求m的值;
(3)若展开式中系数最大项只有第6项和第7项,求m的值.
分析 (1)(x+$\frac{m}{x}$)n展开式的二项式系数之和为256,可得2n=256,解得n即可得出.
(2)$(x+\frac{m}{x})^{8}$的通项公式:Tr+1=${∁}_{8}^{r}{x}^{8-r}(\frac{m}{x})^{r}$=mr${∁}_{8}^{r}$x8-2r,令8-2r=0,解得r即可得出;
(3)$(x+\frac{m}{x})^{8}$的通项公式:Tr+1=${∁}_{8}^{r}{x}^{8-r}(\frac{m}{x})^{r}$=mr${∁}_{8}^{r}$x8-2r,由于展开式中系数最大项只有第6项和第7项,可得m≠0,T6=m5${∁}_{8}^{5}$x-2,T7=m6${∁}_{8}^{6}$x-4,令系数相等解出即可得出.
解答 解:(1)∵(x+$\frac{m}{x}$)n展开式的二项式系数之和为256,∴2n=256,解得n=8.
(2)$(x+\frac{m}{x})^{8}$的通项公式:Tr+1=${∁}_{8}^{r}{x}^{8-r}(\frac{m}{x})^{r}$=mr${∁}_{8}^{r}$x8-2r,令8-2r=0,解得r=4.
∴m4${∁}_{8}^{4}$=$\frac{35}{8}$,解得m=$±\frac{1}{2}$.
(3)$(x+\frac{m}{x})^{8}$的通项公式:Tr+1=${∁}_{8}^{r}{x}^{8-r}(\frac{m}{x})^{r}$=mr${∁}_{8}^{r}$x8-2r,
∵展开式中系数最大项只有第6项和第7项,∴m≠0,
T6=m5${∁}_{8}^{5}$x-2,T7=m6${∁}_{8}^{6}$x-4,令m5${∁}_{8}^{5}$=m6${∁}_{8}^{6}$,
解得m=2.
点评 本题考查了二项式定理的应用、方程的解法,考查了推理能力与计算能力,属于中档题.

 天天练口算系列答案
天天练口算系列答案| A. | 1 | B. | 2 | C. | $\frac{3\sqrt{2}}{2}$ | D. | $\sqrt{5}$ |
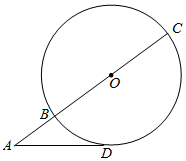 如图,BC为⊙O的直径,且BC=6,延长CB与⊙O在点D处的切线交于点A,若AD=4,则AB=2.
如图,BC为⊙O的直径,且BC=6,延长CB与⊙O在点D处的切线交于点A,若AD=4,则AB=2.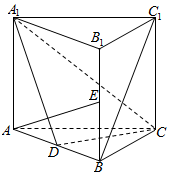 如图,直三棱柱ABC-A1B1C1中,D、E分别是AB、BB1的中点,AB=$\sqrt{2}$,AA1=AC=CB=1.
如图,直三棱柱ABC-A1B1C1中,D、E分别是AB、BB1的中点,AB=$\sqrt{2}$,AA1=AC=CB=1.
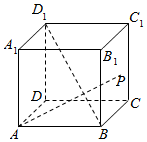 如图,正方体ABCD-A1B1C1D1中,点P在侧面BCC1B1及其边界上运动,并且总是保持AP⊥BD1,试证明动点P在线段B1C上.
如图,正方体ABCD-A1B1C1D1中,点P在侧面BCC1B1及其边界上运动,并且总是保持AP⊥BD1,试证明动点P在线段B1C上.