题目内容
7.函数f(x)=tan(2x+$\frac{π}{3}$),则( )| A. | 函数最小正周期为π,且在(-$\frac{5π}{12}$,$\frac{π}{12}$)是增函数 | |
| B. | 函数最小正周期为$\frac{π}{2}$,且在(-$\frac{5π}{12}$,$\frac{π}{12}$)是减函数 | |
| C. | 函数最小正周期为π,且在($\frac{π}{12}$,$\frac{7π}{12}$)是减函数 | |
| D. | 函数最小正周期为$\frac{π}{2}$,且在($\frac{π}{12}$,$\frac{7π}{12}$)是增函数 |
分析 由条件利用正切函数的周期性和单调性,得出结论.
解答 解:对于函数f(x)=tan(2x+$\frac{π}{3}$),它的最小正周期为$\frac{π}{2}$,
在($\frac{π}{12}$,$\frac{7π}{12}$)上,2x+$\frac{π}{3}$∈($\frac{π}{2}$,$\frac{3π}{2}$),函数f(x)=tan(2x+$\frac{π}{3}$)单调递增,
故选:D.
点评 本题主要考查正切函数的周期性和单调性,属于基础题.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
19.已知角α的顶点在原点,始边与x轴的非负半轴重合,终边交以原点为圆心的单位圆于点A,将角α的终边按逆时针方向旋转$\frac{π}{6}$后交此单位圆于点B,记A(x1,y1),B(x2,y2),若A(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),则x2的值为( )
| A. | -$\frac{\sqrt{3}}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{1}{2}$ |

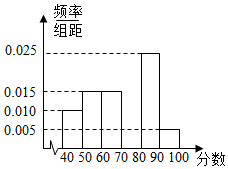 某校从参加高一年级期末考试的学生中抽出40名学生,将其成绩分成六段[40,50),[50,60)…[90,100]后画出如下部分频率分布直方图,观察图形的信息,回答下列问题:
某校从参加高一年级期末考试的学生中抽出40名学生,将其成绩分成六段[40,50),[50,60)…[90,100]后画出如下部分频率分布直方图,观察图形的信息,回答下列问题: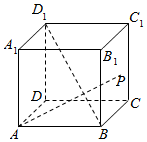 如图,正方体ABCD-A1B1C1D1中,点P在侧面BCC1B1及其边界上运动,并且总是保持AP⊥BD1,试证明动点P在线段B1C上.
如图,正方体ABCD-A1B1C1D1中,点P在侧面BCC1B1及其边界上运动,并且总是保持AP⊥BD1,试证明动点P在线段B1C上.