题目内容
4．sin40°cos20°-cos220°sin20°=$\frac{\sqrt{3}}{2}$．分析 利用诱导公式可得cos220°=-cos40°，利用两角和的正弦函数公式，特殊角的三角函数值即可化简求值得解．
解答 解：∵cos220°=cos（180°+40°）=-cos40°，
∴sin40°cos20°-cos220°sin20°
=sin40°cos20°+cos40°sin20°
=sin（40°+20°）
=sin60°
=$\frac{\sqrt{3}}{2}$．
故答案为：$\frac{\sqrt{3}}{2}$．
点评 本题主要考查了诱导公式，两角和的正弦函数公式，特殊角的三角函数值在三角函数化简求值中的应用，属于基础题．
练习册系列答案
相关题目
19．已知角α的顶点在原点，始边与x轴的非负半轴重合，终边交以原点为圆心的单位圆于点A，将角α的终边按逆时针方向旋转$\frac{π}{6}$后交此单位圆于点B，记A（x1，y1），B（x2，y2），若A（-$\frac{1}{2}$，$\frac{\sqrt{3}}{2}$），则x2的值为（ ）
| A． | -$\frac{\sqrt{3}}{2}$ | B． | -$\frac{1}{2}$ | C． | $\frac{\sqrt{3}}{2}$ | D． | $\frac{1}{2}$ |
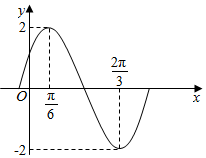函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）（x∈R）的部分图象如图所示．（Ⅰ）求函数f（x）的解析式并求函数f（x）的单调递增区间；
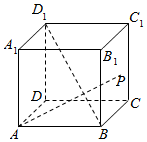如图，正方体ABCD-A1B1C1D1中，点P在侧面BCC1B1及其边界上运动，并且总是保持AP⊥BD1，试证明动点P在线段B1C上．
13．复数z=$\frac{（1-i）^{2}}{3+i}$的所对应的点位于复平面的（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |