题目内容
4.设O为锐角△ABC的外心(三角形外接圆的圆心),$\overrightarrow{AO}$=$\frac{1}{5}$$\overrightarrow{AB}$+$\frac{2}{5}$$\overrightarrow{AC}$,则cos∠BAC等于( )| A. | $\frac{\sqrt{6}}{6}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{6}}{3}$ | D. | $\frac{\sqrt{6}}{4}$ |
分析 分别在$\overrightarrow{AO}$=$\frac{1}{5}$$\overrightarrow{AB}$+$\frac{2}{5}$$\overrightarrow{AC}$两边乘以$\overrightarrow{AB}$,$\overrightarrow{AC}$,联立方程组解出.
解答 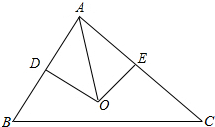 解:取AB中点D,AC中点E,并连接OD,OE,则OD⊥AB,OE⊥AC.
解:取AB中点D,AC中点E,并连接OD,OE,则OD⊥AB,OE⊥AC.
∴cos∠BAO=$\frac{|\overrightarrow{AD}|}{|\overrightarrow{AO}|}=\frac{|\overrightarrow{AB}|}{2|\overrightarrow{AO}|}$,cos∠CAO=$\frac{|\overrightarrow{AE}|}{|\overrightarrow{AO}|}$=$\frac{|\overrightarrow{AC}|}{2|\overrightarrow{AO}|}$.
∴$\overrightarrow{AO}•\overrightarrow{AB}$=|$\overrightarrow{AO}$|•|$\overrightarrow{AB}$|cos∠BAO=$\frac{1}{2}$|$\overrightarrow{AB}$|2,$\overrightarrow{AO}•\overrightarrow{AC}$=|$\overrightarrow{AO}$|•|$\overrightarrow{AC}$|cos∠CAO=$\frac{1}{2}$|$\overrightarrow{AC}$|2.
∵$\overrightarrow{AO}$=$\frac{1}{5}$$\overrightarrow{AB}$+$\frac{2}{5}$$\overrightarrow{AC}$,
∴$\overrightarrow{AO}•\overrightarrow{AB}$=$\frac{1}{5}$|$\overrightarrow{AB}$|2+$\frac{2}{5}$|$\overrightarrow{AB}$|•|$\overrightarrow{AC}$|cos∠BAC,
$\overrightarrow{AO}•\overrightarrow{AC}$=$\frac{1}{5}$|$\overrightarrow{AB}$|•|$\overrightarrow{AC}$|cos∠BAC+$\frac{2}{5}$|$\overrightarrow{AC}$|2.
∴$\frac{1}{2}$|$\overrightarrow{AB}$|2=$\frac{1}{5}$|$\overrightarrow{AB}$|2+$\frac{2}{5}$|$\overrightarrow{AB}$|•|$\overrightarrow{AC}$|cos∠BAC,
$\frac{1}{2}$|$\overrightarrow{AC}$|2=$\frac{1}{5}$|$\overrightarrow{AB}$|•|$\overrightarrow{AC}$|cos∠BAC+$\frac{2}{5}$|$\overrightarrow{AC}$|2.
∴3|$\overrightarrow{AB}$|=4|$\overrightarrow{AC}$|cos∠BAC,|$\overrightarrow{AC}$|=2|$\overrightarrow{AB}$|cos∠BAC.
∴cos2∠BAC=$\frac{3}{8}$,∵$∠BAC<\frac{π}{2}$,
∴cos∠BAC=$\sqrt{\frac{3}{8}}$=$\frac{\sqrt{6}}{4}$.
故选:D.
点评 本题考查了平面向量数量积的计算,构造方程组是关键.

| A. | 4 | B. | 2 | C. | 1 | D. | -4 |
| A. | 15° | B. | 30° | C. | 45° | D. | 60° |
| A. | $\frac{\sqrt{6}}{4}$ | B. | $\frac{\sqrt{6}-\sqrt{2}}{4}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{4}$ |
| A. | -$\frac{1}{2}$<a<1 | B. | -$\frac{1}{2}$<a<0 | C. | 0<a<1 | D. | -$\frac{1}{2}$<a<0或$\frac{1}{2}$<a<1 |