题目内容
11.在△ABC中,a,b,c分别是角A,B,C的对边,已知3(b2+c2)=3a2+2bc.(1)求sinA的值;
(2)若a=2,△ABC的面积S=$\frac{{\sqrt{2}}}{2}$,且b>c,求b和c的值.
分析 (1)利用余弦定理即可得出.
(2)利用三角形面积计算公式、余弦定理即可得出.
解答 解:(1)由3(b2+c2)=3a2+2bc.
∴cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$=$\frac{\frac{2}{3}bc}{2bc}$=$\frac{1}{3}$,
∵A∈(0,π),
∴sinA=$\sqrt{1-co{s}^{2}A}$=$\frac{2\sqrt{2}}{3}$.
(2)∵$S=\frac{{\sqrt{2}}}{2}⇒\frac{1}{2}bcsinA=\frac{{\sqrt{2}}}{2}$,
又$sinA=\frac{{2\sqrt{2}}}{3}⇒bc=\frac{3}{2}$ ①
由余弦定理a2=b2+c2-2bccosA⇒b2+c2=5,
②∵b>c,联立①②可得$b=\frac{{3\sqrt{2}}}{2},c=\frac{{\sqrt{2}}}{2}$.
点评 本题考查了三角形面积计算公式、余弦定理,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
11.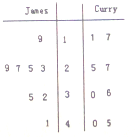 如图是NBA15-16季后赛中勒布朗-詹姆斯(LeBron James)与斯蒂芬-库里(Stephen Curry)随机抽取的8场比赛得分统计结果,则下列说法正确的是( )
如图是NBA15-16季后赛中勒布朗-詹姆斯(LeBron James)与斯蒂芬-库里(Stephen Curry)随机抽取的8场比赛得分统计结果,则下列说法正确的是( )
 如图是NBA15-16季后赛中勒布朗-詹姆斯(LeBron James)与斯蒂芬-库里(Stephen Curry)随机抽取的8场比赛得分统计结果,则下列说法正确的是( )
如图是NBA15-16季后赛中勒布朗-詹姆斯(LeBron James)与斯蒂芬-库里(Stephen Curry)随机抽取的8场比赛得分统计结果,则下列说法正确的是( )| A. | 他们的水平相当,但James 比Curry发挥稳定 | |
| B. | 他们的水平相当,但Curry比James 发挥稳定 | |
| C. | James比Curry水平高,也比Curry发挥稳定 | |
| D. | Curry比水平高,也比James发挥稳定 |
6.已知复数z满足z(3+4i)=5-5i,则复数z在复平面对应的点所在的象限为( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
3.△ABC中,A=$\frac{π}{6}$,b=2,以下错误的是( )
| A. | 若a=1,则c有一解 | B. | 若a=$\sqrt{3}$,则c有两解 | ||
| C. | 若a=$\frac{11}{6}$,则c有两解 | D. | 若a=3,则c有两解 |
1.对于任意的实数a,b,c,下列命题正确的是( )
| A. | 若a>b,c=0,则ac>bc | B. | 若ac2>bc2,则a>b | ||
| C. | 若a>b,则$\frac{1}{a}$>$\frac{1}{b}$ | D. | 若a>b,则ac2>bc2 | ||
| E. | 若a>b,则ac2>bc2 |