题目内容
13.有一个五边形ABCDE,若把顶点A,B,C,D,E涂上红、黄、绿三种颜色中的一种,使得相邻的顶点所涂的颜色不同,则共有30种不同的涂色方法.分析 本题需要分类来解答,首先A选取一种颜色,有3种情况.如果A的两个相邻点颜色相同,2种情况,这时最后两个边也有2种情况;如果A的两个相邻点颜色不同,2种情况,最后两个边有3种情况.根据计数原理得到结果.
解答 解:由题意知本题需要分类来解答,
首先A选取一种颜色,有3种情况.
如果A的两个相邻点颜色相同,2种情况;
这时最后两个边也有2种情况;
如果A的两个相邻点颜色不同,2种情况;
这时最后两个边有3种情况.
∴方法共有3(2×2+2×3)=30种.
故答案为:30.
点评 对于复杂一点的计数问题,有时分类以后,每类方法并不都是一步完成的,必须在分类后又分步,综合利用两个原理解决,即类中有步,步中有类.

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案
相关题目
3.设变量x,y满足约束条件:$\left\{\begin{array}{l}x+y-3≥0\\ x-y+1≥0\\ 2x-y-3≤0\end{array}\right.$,则目标函数z=2x+3y+4的最小值为( )
| A. | 10 | B. | 11 | C. | 12 | D. | 27 |
5.数列{an}满足:an+1=λan-1(n∈N*,λ∈R且λ≠0),若数列{an-1}是等比数列,则λ的值等于( )
| A. | 1 | B. | -1 | C. | $\frac{1}{2}$ | D. | 2 |
3.用1,2,3,4四个数字组成一个四位数,其中大于3300的偶数有多少个( )
| A. | 128 | B. | 64 | C. | 96 | D. | 48 |
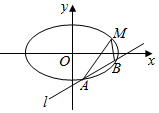 ⑧如图,已知椭圆的中心在原点,焦点在x轴上,离心率为$\frac{\sqrt{3}}{2}$,且经过点M(4,1),直线l:y=x+m交椭圆与A,B两不同的点.
⑧如图,已知椭圆的中心在原点,焦点在x轴上,离心率为$\frac{\sqrt{3}}{2}$,且经过点M(4,1),直线l:y=x+m交椭圆与A,B两不同的点.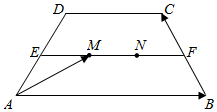 如图,已知四边形ABCD是等腰梯形,E、F分别是腰AD、BC的中点,M、N是线段EF上的两个点,且EM=MN=NF,下底是上底的2倍,若$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,求$\overrightarrow{AM}$.
如图,已知四边形ABCD是等腰梯形,E、F分别是腰AD、BC的中点,M、N是线段EF上的两个点,且EM=MN=NF,下底是上底的2倍,若$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,求$\overrightarrow{AM}$.