题目内容
4.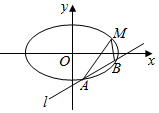 ⑧如图,已知椭圆的中心在原点,焦点在x轴上,离心率为$\frac{\sqrt{3}}{2}$,且经过点M(4,1),直线l:y=x+m交椭圆与A,B两不同的点.
⑧如图,已知椭圆的中心在原点,焦点在x轴上,离心率为$\frac{\sqrt{3}}{2}$,且经过点M(4,1),直线l:y=x+m交椭圆与A,B两不同的点.(1)求椭圆的方程;
(2)若直线l不经过点M,试问直线MA,MB与x轴能否围成一个等腰三角形?证明你的结论.
分析 (1)设出椭圆的标准方程,根据椭圆的离心率为$\frac{\sqrt{3}}{2}$,得出a2=4b2,再根据M(4,1)在椭圆上,解方程组得b2=5,a2=20,从而得出椭圆的方程;
(2)因为直线l:y=x+m交椭圆于不同的两点A,B,可将直线方程与椭圆方程消去y得到关于x的方程,有两个不相等的实数根,从而△>0,解得-5<m<5;设出A(x1,y1),B(x2,y2),由根与系数的关系再计算出直线MA的斜率k1,MB的斜率为k2,将式子k1+k2通分化简,最后可得其分子为0,从而得出k1+k2=0,得直线MA,MB的倾斜角互补,命题得证.
解答 解:(1)设椭圆的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),
∵椭圆的离心率为e=$\frac{c}{a}$=$\frac{\sqrt{3}}{2}$,即c=$\frac{\sqrt{3}}{2}$a,
a2-c2=b2,
∴a2=4b2,
又∵M(4,1),
∴$\frac{16}{{a}^{2}}$+$\frac{1}{{b}^{2}}$=1,解得b2=5,a2=20,
故椭圆方程为$\frac{{x}^{2}}{20}$+$\frac{{y}^{2}}{5}$=1;
(2)将y=x+m代入x2+4y2=20,
并整理得5x2+8mx+4m2-20=0,
∵直线l:y=x+m交椭圆于不同的两点A,B,
∴△=(8m)2-20(4m2-20)>0,解得-5<m<5;
设直线MA,MB的斜率分别为k1和k2,只要证明k1+k2=0.
设A(x1,y1),B(x2,y2),
利用根与系数的关系得:x1+x2=-$\frac{8m}{5}$,x1x2=$\frac{4{m}^{2}-20}{5}$.
k1+k2=$\frac{{y}_{1}-1}{{x}_{1}-4}$+$\frac{{y}_{2}-1}{{x}_{2}-4}$=$\frac{({y}_{1}-1)({x}_{2}-4)+({y}_{2}-1)({x}_{1}-4)}{({x}_{1}-4)({x}_{2}-4)}$,
上式的分子=(x1+m-1)(x2-4)+(x2+m-1)(x1-4)
=2x1x2+(m-5)(x1+x2)-8(m-1)
=$\frac{2(4{m}^{2}-20)}{5}$-$\frac{8m(m-5)}{5}$-8(m-1)=0,
所以k1+k2=0,得直线MA,MB的倾斜角互补,
∴直线MA、MB与x轴围成一个等腰三角形.
点评 本题考查了椭圆的方程和直线与椭圆的位置关系等知识点,解题时注意设而不求和转化化归等常用思想的运用,本题的综合性较强对运算的要求很高.

| A. | ($\frac{1}{2}$,$\frac{4}{3}$) | B. | [$\frac{4}{3}$,4] | C. | [$\frac{4}{3}$,3) | D. | [$\frac{1}{2}$,4] |
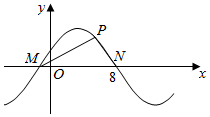 如图所示,M,N是函数y=2sin(ωx+ϕ)(ω>0)图象与x轴的交点,点P在M,N之间的图象上运动,当△MPN面积最大时,PM⊥PN,则ω=( )
如图所示,M,N是函数y=2sin(ωx+ϕ)(ω>0)图象与x轴的交点,点P在M,N之间的图象上运动,当△MPN面积最大时,PM⊥PN,则ω=( )| A. | $\frac{π}{4}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{2}$ | D. | 8 |
 已知抛物线C:x2=4y,F为抛物线焦点,圆E:x2+(y+1)2=1,斜率为k(k>0)的直线l与抛物线C和圆E都相切,切点分别为P和Q,直线PF和PQ分别交x轴于点M,N.
已知抛物线C:x2=4y,F为抛物线焦点,圆E:x2+(y+1)2=1,斜率为k(k>0)的直线l与抛物线C和圆E都相切,切点分别为P和Q,直线PF和PQ分别交x轴于点M,N.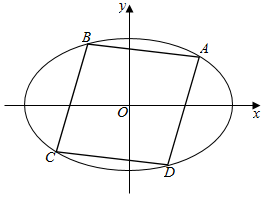 如图,在平面直角坐标系xOy中,设椭圆$\frac{{x}^{2}}{4}$+y2=1的所有内接菱形构成的集合为F.
如图,在平面直角坐标系xOy中,设椭圆$\frac{{x}^{2}}{4}$+y2=1的所有内接菱形构成的集合为F.