题目内容
2.六本不同的书,按照以下要求处理,各有几种分法?(1)分三堆,一堆一本,一堆两本,一堆三本;
(2)甲得一本,乙得两本,丙得三本;
(3)一人得一本,一人得两本,一人得三本;
(4)平均分给甲、乙、丙三人,每人两本;
(5)平均分成三堆,每堆两本.
分析 根据分组分配问题的原则,先合理的分组,再分配即可,注意平均分组的问题
解答 解:(1)无序不均匀分组问题.先选1本有C16种选法;再从余下的5本中选2本有C25种选法;最后余下3本全选有C33种方法,故共有C16C25C33=60种.
(2)甲选1本有C16种选法;乙再从余下的5本中选2本有C25种选法;丙最后余下3本全选有C33种方法,故共有C16C25C33=60种
(3)在第(1)题基础上,还应考虑再分配,共有C16C25C33A33=360种,
(4)有序均匀分组,6本不同的书平均分成三堆,有$\frac{{C}_{6}^{2}{C}_{4}^{2}}{{A}_{3}^{3}}$=15种分堆方法,由于甲、乙、丙是不同的三人,还应考虑再分配,共有15A33=90种
(5)有序均匀分组,6本不同的书平均分成三堆,有$\frac{{C}_{6}^{2}{C}_{4}^{2}}{{A}_{3}^{3}}$=15种分堆方法.
点评 本题考查排列、组合及简单计数问题,正确区分无序不均匀分组问题.有序不均匀分组问题.无序均匀分组问题.是解好组合问题的一部分;本题考查计算能力,理解能力.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
12.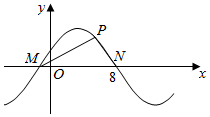 如图所示,M,N是函数y=2sin(ωx+ϕ)(ω>0)图象与x轴的交点,点P在M,N之间的图象上运动,当△MPN面积最大时,PM⊥PN,则ω=( )
如图所示,M,N是函数y=2sin(ωx+ϕ)(ω>0)图象与x轴的交点,点P在M,N之间的图象上运动,当△MPN面积最大时,PM⊥PN,则ω=( )
 如图所示,M,N是函数y=2sin(ωx+ϕ)(ω>0)图象与x轴的交点,点P在M,N之间的图象上运动,当△MPN面积最大时,PM⊥PN,则ω=( )
如图所示,M,N是函数y=2sin(ωx+ϕ)(ω>0)图象与x轴的交点,点P在M,N之间的图象上运动,当△MPN面积最大时,PM⊥PN,则ω=( )| A. | $\frac{π}{4}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{2}$ | D. | 8 |
17.三角形的一个内角为60°是这个三角形三内角成等差数列的( )条件.
| A. | 充分不必要 | B. | 必要不充分 | ||
| C. | 充要 | D. | 既不充分也不必要 |
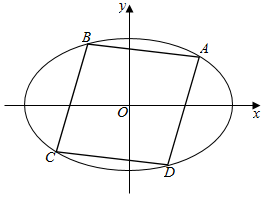 如图,在平面直角坐标系xOy中,设椭圆$\frac{{x}^{2}}{4}$+y2=1的所有内接菱形构成的集合为F.
如图,在平面直角坐标系xOy中,设椭圆$\frac{{x}^{2}}{4}$+y2=1的所有内接菱形构成的集合为F.