题目内容
13.已知函数f(x)=|x-m|+|x-2|.(1)当m=1时,求不等式f(x)≥3的解集;
(2)若不等式f(x)≥4-x对?x∈R恒成立,求实数m的取值范围.
分析 (1)根据绝对值不等式的解法进行求解即可.
(2)根据f(x)≥4-x恒成立,进行转化,构造函数利用数形结合进行比较即可得到结论.
解答 解:(1)当m=1时,f(x)=|x-1|+|x-2|.
不等式f(x)≥3等价为|x-1|+|x-2|≥3.
若x≤1,则不等式等价为-(x-1)-(x-2)≥3,
即-2x≥0,得x≤0,此时x≤0,
若1<x<2,则不等式等价为x-1-(x-2)≥3,即1≥3,此时不等式无解,
若x≥2,则不等式等价为x-1+x-2≥3,
即2x≥6,得x≥3,此时x≥3,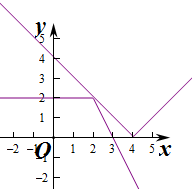
综上x≥3或x≤0,即不等式的解集为(-∞,0]∪[3,+∞)
(2)若不等式f(x)≥4-x对?x∈R恒成立,
即|x-m|+|x-2|≥4-x对?x∈R恒成立.
即|x-m|≥-|x-2|+4-x
设g(x)=-|x-2|+4-x,
则g(x)=$\left\{\begin{array}{l}{2,}&{x≤2}\\{-2x+6,}&{x>2}\end{array}\right.$,
作出函数g(x)和h(x)=|x-m|的图象如图:
若h(x)≥g(x)恒成立,
则只要h(2)≥2且m≥3,
即|2-m|≥2,且m≥3,
得m≥4或m≤0,
∵m≥3,
∴m≥4,
即实数m的取值范围[4,+∞).
点评 本题主要考查绝对值不等式的解法以及不等式恒成立问题,利用分类讨论和数形结合的数学思想是解决本题的关键.

练习册系列答案
相关题目
1.下列命题的说法错误的是( )
| A. | 若p∧q为假命题,则p,q均为假命题 | |
| B. | 命题“?x∈R,x2+x+1>0”为真命题. | |
| C. | “x=-1”是“x2-3x+2>0”的充分不必要条件 | |
| D. | 命题“若x2-3x+2=0,则 x=1”的逆否命题为:“若x≠1,则x2-3x+2≠0” |
18.正数a,b满足a-2ab+b=0,则2a+b的最小值为( )
| A. | $\frac{3}{2}+\sqrt{2}$ | B. | $2\sqrt{2}$ | C. | $1+\sqrt{2}$ | D. | 3 |
5.已知函数f(x)=$\left\{\begin{array}{l}{log_{\frac{1}{2}}}x,x>0\\{4^x},x≤0\end{array}$,则f[f(-2)]-16f[f(4)]=( )
| A. | -3 | B. | 3 | C. | -6 | D. | 6 |
3.已知i为虚数单位,复数z满足z(1-i)=1+i,则z2016=( )
| A. | 1 | B. | -1 | C. | i | D. | -i |