题目内容
5．已知函数f（x）=$\left\{\begin{array}{l}{log_{\frac{1}{2}}}x，x＞0\\{4^x}，x≤0\end{array}$，则f[f（-2）]-16f[f（4）]=（ ）| A． | -3 | B． | 3 | C． | -6 | D． | 6 |
分析 先利用分段函数的性质求出f（-2），f（4），再求出f[f（-2）]，f[f（4）]，由此能求出f[f（-2）]-16f[f（4）]的值．
解答 解：∵函数f（x）=$\left\{\begin{array}{l}{log_{\frac{1}{2}}}x，x＞0\\{4^x}，x≤0\end{array}$，
∴f（-2）=4-2=$\frac{1}{16}$，
f[f（-2）]=f（$\frac{1}{16}$）=$lo{g}_{\frac{1}{2}}\frac{1}{16}$=4，
f（4）=$lo{g}_{\frac{1}{2}}4$=-2，
f[f（4）]=4-2=$\frac{1}{16}$，
f[f（-2）]-16f[f（4）]=4-16×$\frac{1}{16}$=3．
故选：B．
点评 本题考查函数值的求法，是基础题，解题时要认真审题，注意分段函数的性质的合理运用．
练习册系列答案
相关题目
17．若cos（α+$\frac{π}{2}$）=-$\frac{1}{2}$，α∈（$\frac{π}{2}$，π），则cos（π-α）值为（ ）
| A． | $\frac{{\sqrt{3}}}{2}$ | B． | $\frac{1}{2}$ | C． | $-\frac{{\sqrt{3}}}{2}$ | D． | $-\frac{1}{2}$ |
14．已知f（x）=sin（x+1）$\frac{π}{3}$-$\sqrt{3}$cos（x+1）$\frac{π}{3}$，则f（1）+f（2）+f（3）+…+f（2011）=（ ）
| A． | 2$\sqrt{3}$ | B． | $\sqrt{3}$ | C． | -$\sqrt{3}$ | D． | 0 |
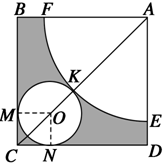如图所示，在边长为$5+\sqrt{2}$的正方形ABCD中，以A为圆心画一个扇形，以O为圆心画一个圆，M，N，K为切点，以扇形为圆锥的侧面，以圆O为圆锥底面，围成一个圆锥，求圆锥的表面积与体积．