题目内容
19.圆C1:x2+y2-2mx+4y+m2-5=0,圆C2:x2+y2+2x-2my+m2-3=0,当圆C1与圆C2内切时,m的取值是-2或-1.分析 先分别求出两圆的圆心和半径,再求出圆心距,利用两圆内切的性质能求出结果.
解答 解:∵圆C1:x2+y2-2mx+4y+m2-5=0,圆C2:x2+y2+2x-2my+m2-3=0,
∴圆C1的圆心C1(m,-2),半径r1=$\frac{1}{2}\sqrt{4{m}^{2}+16-4{m}^{2}+20}$=3,
圆C2的C2(-1,m),半径r=$\frac{1}{2}\sqrt{4+4{m}^{2}-4{m}^{2}+12}$=2,
∴|C1C2|=$\sqrt{(m+1)^{2}+(-2-m)^{2}}$=$\sqrt{2{m}^{2}+6m+5}$,
∵圆C1与圆C2内切,
∴|C1C2|=|r1-r2|=|3-2|=1,
∴$\sqrt{2{m}^{2}+6m+5}$=1,
解得m=-2或m=-1.
故答案为:-2或1.
点评 本题考查实数值的求法,是基础题,解题时要认真审题,注意两圆内切的性质和两点间距离公式的合理运用.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
7.P是椭圆$\frac{x^2}{4}+\frac{y^2}{2}=1$上的一点,F1、F2分别是左右焦点,若|PF1|=3|PF2|,则过点P的椭圆的切线的斜率是( )
| A. | $±\sqrt{2}$ | B. | $±\frac{{\sqrt{2}}}{3}$ | C. | $±\frac{{\sqrt{2}}}{4}$ | D. | $±\frac{{\sqrt{2}}}{2}$ |
14.已知A(2,3),B(-4,0),P(-3,1),Q(-1,2),试判断直线AB与PQ的位置关系( )
| A. | 平行 | B. | 垂直 | C. | 重合 | D. | 不能确定 |
4.若3a+4b=ab,a>0且b>0,则a+b的最小值是( )
| A. | $6+2\sqrt{3}$ | B. | $7+2\sqrt{3}$ | C. | $6+4\sqrt{3}$ | D. | $7+4\sqrt{3}$ |
9.“x<4”是“$\sqrt{x}$<2”的( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既非充分又非必要条件 |
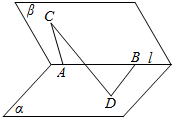 如图,在二面角α-l-β的棱l上有A,B两点,直线AC,BD分别在这个二面角的两个半平面内,且都垂直于AB,若二面角α-l-β的大小为$\frac{π}{3}$,AB=AC=2,CD=$\sqrt{11}$,则BD=3.
如图,在二面角α-l-β的棱l上有A,B两点,直线AC,BD分别在这个二面角的两个半平面内,且都垂直于AB,若二面角α-l-β的大小为$\frac{π}{3}$,AB=AC=2,CD=$\sqrt{11}$,则BD=3.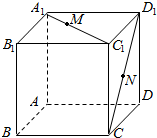 在长方体ABCD-A1B1C1D1中,|AB|=|AD|=3,|AA1|=3,点M在A1C1上,|MC1|=2|A1M|,N在D1C上且为D1C的中点,求M,N两点间的距离.
在长方体ABCD-A1B1C1D1中,|AB|=|AD|=3,|AA1|=3,点M在A1C1上,|MC1|=2|A1M|,N在D1C上且为D1C的中点,求M,N两点间的距离.