题目内容
18.给定平面内三个向量$\overrightarrow a=(3,2),\overrightarrow b=(-1,2),\overrightarrow c=(4,1)$(1)若($(\overrightarrow a+k\overrightarrow c)∥(2\overrightarrow b+n\overrightarrow c)$,求实数k;
(2)求满足$\overrightarrow a=m\overrightarrow b-n\overrightarrow c$的实数m,n.
分析 (1)根据向量的坐标运算和向量的平行即可得到关于k的方程,解得即可
(2)利用向量的线性运算法则及向量相等即可得出.
解答 解:(1)$\overrightarrow{a}$+k$\overrightarrow{c}$=(3,2)+k(4,1)=(3+4k,2+k),
2$\overrightarrow{b}$+$\overrightarrow{c}$=2(-1,2)+(4,1)=(2,5),
∵$(\overrightarrow a+k\overrightarrow c)∥(2\overrightarrow b+n\overrightarrow c)$,
∴5(3+4k)=2(2+k),
解得k=-$\frac{11}{18}$,
(2)$\overrightarrow a=m\overrightarrow b-n\overrightarrow c$,
∴(3,2)=m(-1,2)-n(4,1)=(-m-4n,2m-n),
∴$\left\{\begin{array}{l}{3=-m-4n}\\{2=2m-n}\end{array}\right.$,
解得m=$\frac{5}{9}$,n=-$\frac{8}{9}$
点评 本题考查了向量坐标形式的加减法和数乘法则的综合运算,向量共线的坐标条件,直接代入公式求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.在△ABC中,∠A=60°,b=1,S△ABC=$\sqrt{3}$,则$\frac{a-2b+c}{sinA-2sinB+sinC}$的值等于( )
| A. | $\frac{{2\sqrt{39}}}{3}$ | B. | $\frac{26}{3}\sqrt{3}$ | C. | $\frac{8}{3}\sqrt{3}$ | D. | $2\sqrt{3}$ |
13.已知α是第三象限角且$|{cos\frac{α}{3}}|=-cos\frac{α}{3}$,则$\frac{α}{3}$角是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
10.已知对任意实数x,有f(-x)=-f(x),g(-x)=g(x),且x<0时,导函数分别满足f′(x)>0,g′(x)<0,则x>0时,成立的是( )
| A. | f′(x)>0,g′(x)<0 | B. | f′(x)>0,g′(x)>0 | C. | f′(x)<0,g′(x)<0 | D. | f′(x)<0,g′(x)>0 |
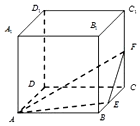 如图,在棱长为1的正方体ABCD-A1B1C1D1中,点E,F分别是棱BC,CC1的中点,P是侧面BCC1B1内一点,若A1P∥平面AEF,则线段AP长度的取值范围是[$\frac{3\sqrt{2}}{4}$,$\frac{\sqrt{5}}{2}$].
如图,在棱长为1的正方体ABCD-A1B1C1D1中,点E,F分别是棱BC,CC1的中点,P是侧面BCC1B1内一点,若A1P∥平面AEF,则线段AP长度的取值范围是[$\frac{3\sqrt{2}}{4}$,$\frac{\sqrt{5}}{2}$].