题目内容
19.已知实数x,y满足$\left\{\begin{array}{l}y-1≥0\\ y-1≤2(x-1)\\ x+y-5≤0\end{array}\right.$,目标函数z=x-y的最小值为-1.分析 先画出约束条件的可行域,再将可行域中各个角点的值依次代入目标函数z=x-y,不难求出目标函数z=x-y的最小值.
解答 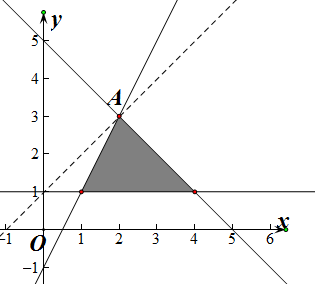 解:如图作出阴影部分即为满足约束条件足$\left\{\begin{array}{l}y-1≥0\\ y-1≤2(x-1)\\ x+y-5≤0\end{array}\right.$的可行域,
解:如图作出阴影部分即为满足约束条件足$\left\{\begin{array}{l}y-1≥0\\ y-1≤2(x-1)\\ x+y-5≤0\end{array}\right.$的可行域,
由得A(2,3),
当直线z=x-y平移到点A时,
直线z=x-y在y轴上的截距最大,即z取最小值,
即当x=2,y=3时,z=x-y取最小值为-1.
故答案为:-1.
点评 本题主要考查线性规划的基本知识,用图解法解决线性规划问题时,利用线性规划求函数的最值时,关键是将目标函数赋予几何意义.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
14.已知函数$f(x)=sin(\frac{π}{3}x+φ)(|φ|<\frac{π}{2})$的图象关于直线x=1对称,把f(x)的图象向右平移3个单位长度后,所得图象对应的函数解析式为( )
| A. | y=sin($\frac{π}{3}$x+$\frac{π}{6}$) | B. | y=sin($\frac{π}{3}$x-$\frac{π}{6}$) | C. | y=cos($\frac{π}{3}$x+$\frac{π}{6}$) | D. | y=sin($\frac{π}{3}$x-$\frac{5π}{6}$) |
4.已知a∈R,若不等式lnx-$\frac{a}{x}$+x-2>0对于任意x∈(1,+∞)恒成立,则a的取值范围为( )
| A. | a≤2 | B. | a≤1 | C. | a≤-1 | D. | a≤0 |
11.一条光线从点(-2,-3)射出,经y轴反射后与圆(x+3)2+(y-2)2=1相切,则入射光线所在直线的斜率为( )
| A. | $\frac{3}{2}$或$\frac{2}{3}$ | B. | $\frac{4}{3}$或$\frac{3}{4}$ | C. | $\frac{5}{3}或\frac{3}{5}$ | D. | $\frac{5}{4}或\frac{4}{5}$ |
8.直线x-y=0与圆x2+y2=1的位置关系是( )
| A. | 相切 | B. | 相离 | ||
| C. | 相交且直线过圆心 | D. | 相交且直线不过圆心 |
9.已知变量x与y负相关,且由观测数据计算得样本平均数$\overline x=4,\overline y=6.5$,则由该观测数据算得的线性回归方程可能是( )
| A. | y=2x-1.5 | B. | y=0.8x+3.3 | C. | y=-2x+14.5 | D. | y=-0.6x+9.1 |
