题目内容
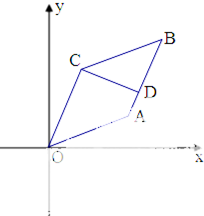如图，在平行四边形OABC中，已知点A（3，1），C（1，3）．（1）求AB所在直线的方程；
（2）过点C作CD⊥AB于点D，求CD所在直线的方程．
考点：直线的一般式方程
专题：直线与圆
分析：（1）利用相互平行的直线斜率之间的关系即可得出；
（2）利用相互垂直的直线斜率之间的关系即可得出．
（2）利用相互垂直的直线斜率之间的关系即可得出．
解答：
解：（1）kOC=
=3，∵AB∥OC，∴kAB=kOC=3．
∴AB所在直线的方程为y-1=3（x-3），化为3x-y-8=0．
（2）∵CD⊥AB，∴kAB•kCD=-1，
∴kCD=-
．
∴直线CD的方程为y-3=-
（x-1），
化为x+3y-10=0．
| 3 |
| 1 |
∴AB所在直线的方程为y-1=3（x-3），化为3x-y-8=0．
（2）∵CD⊥AB，∴kAB•kCD=-1，
∴kCD=-
| 1 |
| 3 |
∴直线CD的方程为y-3=-
| 1 |
| 3 |
化为x+3y-10=0．
点评：本题考查了平行四边形的性质、相互平行垂直的直线斜率之间的关系，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
函数y=
的单调递增区间为（ ）
| x2-3x+2 |
A、[
| ||
B、（-∞，
| ||
| C、[2，+∞） | ||
| D、（-∞，1] |
函数f（x）=
，若0＜f （x0）＜1，则x0的取值范围是（ ）
|
| A、[1，+∞） |
| B、（1，+∞） |
| C、（-∞，1] |
| D、（0，+∞） |