题目内容
已知数列{an}的前n项和为Sn=10n-n2.
(1)求数列{an}的通项公式;
(2)若bn=|an|,求数列{bn}的前n项和Tn.
(1)求数列{an}的通项公式;
(2)若bn=|an|,求数列{bn}的前n项和Tn.
考点:数列的求和,数列递推式
专题:等差数列与等比数列
分析:(1)利用“当n=1时,a1=S1;当n≥2时,an=Sn-Sn-1”即可得出.
(2)根据an和的bn表达式,然后根据式子的特点求数列{bn}的前n项和Tn.
(2)根据an和的bn表达式,然后根据式子的特点求数列{bn}的前n项和Tn.
解答:
解:(1)当n=1时,a1=S1=9,
当n≥2时,an=Sn-Sn-1=10n-n2-[10(n-1)-(n-1)2]
=11-2n,
当n=1时,a1=9,满足an=11-2n,
所以an=11-2n,n∈N*,
(2)∵an=11-2n,n∈N*,
当n≤5时,an>0; 当n≥6时,an<0,
①当n≤5时,和Tn=|a1|+|a2|+…+|an|=a1+a2+…+an=Sn=10n-n2.
②当n≥6时,Tn=|a1|+|a2|+…+|an|=2(a1+a2+…+a5)-(a1+a2+…+an)=2S5-Sn=n2-10n+50,
所以Tn=
当n≥2时,an=Sn-Sn-1=10n-n2-[10(n-1)-(n-1)2]
=11-2n,
当n=1时,a1=9,满足an=11-2n,
所以an=11-2n,n∈N*,
(2)∵an=11-2n,n∈N*,
当n≤5时,an>0; 当n≥6时,an<0,
①当n≤5时,和Tn=|a1|+|a2|+…+|an|=a1+a2+…+an=Sn=10n-n2.
②当n≥6时,Tn=|a1|+|a2|+…+|an|=2(a1+a2+…+a5)-(a1+a2+…+an)=2S5-Sn=n2-10n+50,
所以Tn=
|
点评:本题主要考查数列求和的计算,根据条件求出an和的bn表达式是解决本题的关键,注意要对n进行讨论.

练习册系列答案
相关题目
已知f(x)是定义在R上的奇函数,且当x≥0时,f(x)=x2,对任意的x∈[t,t+2]不等式f(x+t)≥2f(x)恒成立,那么实数t的取值范围是( )
A、[
| ||
| B、[2,+∞) | ||
C、(0,
| ||
D、[0,
|
直线MN与双曲线C:
-
=1的左右支分别交于M、N点,与双曲线C的右准线相交于P点,F为右焦点,若|
|=2|
|,又
=λ
(λ∈R),则实数λ的值为( )
| x2 |
| a2 |
| y2 |
| b2 |
| FM |
| FN |
| NP |
| PM |
A、
| ||
| B、1 | ||
| C、2 | ||
D、
|
 如图所示.△ABC是边长为1的正三角形,△BDC是顶角∠BDC=120°的等腰三角形,以D为顶点作一个60°角,角的两边分别交AB,AC于M,N,连接MN,求△AMN的周长.
如图所示.△ABC是边长为1的正三角形,△BDC是顶角∠BDC=120°的等腰三角形,以D为顶点作一个60°角,角的两边分别交AB,AC于M,N,连接MN,求△AMN的周长.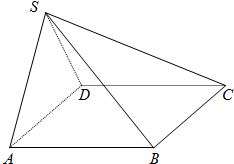 如图,在四棱锥S-ABCD中,底面ABCD是边长为a的正方形,侧面SAD为正三角形,且垂直于底面ABCD.
如图,在四棱锥S-ABCD中,底面ABCD是边长为a的正方形,侧面SAD为正三角形,且垂直于底面ABCD.