题目内容
已知函数y=|x|.
(1)作出函数图象
(2)判断函数的奇偶性.
(3)若x∈[-2,1],求函数的最小值与最大值.
(1)作出函数图象
(2)判断函数的奇偶性.
(3)若x∈[-2,1],求函数的最小值与最大值.
考点:奇偶性与单调性的综合,函数的最值及其几何意义,函数奇偶性的判断,函数的图象
专题:函数的性质及应用
分析:(1)将函数进行化简,即可作出函数图象
(2)根据函数的奇偶性的定义或图象特点即可判断函数的奇偶性.
(3)若x∈[-2,1],根据函数的单调性和图象即可求函数的最小值与最大值.
(2)根据函数的奇偶性的定义或图象特点即可判断函数的奇偶性.
(3)若x∈[-2,1],根据函数的单调性和图象即可求函数的最小值与最大值.
解答:
解:(1)y=|x|=
,则对应的函数图象为: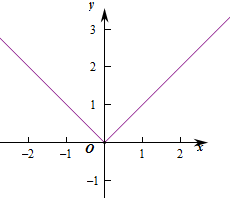
(2)函数f(x)的定义域为R,
∵f(-x)=|-x|=|x|=f(x),
∴f(-x)=f(x),即函数是偶函数.
(3)若x∈[-2,1],∵函数f(x)是偶函数,∴关于y轴对称,
∴函数的最小值与f(0)=0,最大值为f(-2)=|-2|=2.
|

(2)函数f(x)的定义域为R,
∵f(-x)=|-x|=|x|=f(x),
∴f(-x)=f(x),即函数是偶函数.
(3)若x∈[-2,1],∵函数f(x)是偶函数,∴关于y轴对称,
∴函数的最小值与f(0)=0,最大值为f(-2)=|-2|=2.
点评:本题主要考查函数图象的做法,以及函数奇偶性和单调性的判断和应用,要求熟练掌握相应的定义,比较基础.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,A,B是双曲线
如图,A,B是双曲线