题目内容
化简:
(1)
sinx+
cosx;
(2)
cosx-
sinx;
(3)
sin
+cos
;
(4)
sin(
-x)+
cos(
-x);
(5)sin347°cos148°+sin77°cos58°;
(6)sin164°sin224°+sin254°sin314°;
(7)sin(α+β)cos(γ-β)-cos(β+α)sin(β-γ);
(8)sin(α-β)sin(β-γ)-cos(α-β)cos(γ-β);
(9)
;
(10)
.
(1)
| 15 |
| 5 |
(2)
| 3 |
| 2 |
| ||
| 2 |
(3)
| 3 |
| x |
| 2 |
| x |
| 2 |
(4)
| ||
| 4 |
| π |
| 4 |
| ||
| 4 |
| π |
| 4 |
(5)sin347°cos148°+sin77°cos58°;
(6)sin164°sin224°+sin254°sin314°;
(7)sin(α+β)cos(γ-β)-cos(β+α)sin(β-γ);
(8)sin(α-β)sin(β-γ)-cos(α-β)cos(γ-β);
(9)
tan
| ||||
1-tan
|
(10)
| sin(α+β)-2sinαcosβ |
| 2sinαsinβ+cos(α+β) |
考点:两角和与差的正切函数,两角和与差的正弦函数
专题:三角函数的求值
分析:由两角和与差的正切函数公式和两角和与差的正弦函数公式化简即可.
解答:
解:(1)
sinx+
cosx=2
sin(x+
);
(2)
cosx-
sinx=
sin(
-x);
(3)
sin
+cos
=2sin(
+
);
(4)
sin(
-x)+
cos(
-x)=
sin(
-x+
)=
sin(
-x);
(5)sin347°cos148°+sin77°cos58°=sin13°cos32°+cos13°sin32°=sin45°=
;
(6)sin164°sin224°+sin254°sin314°=-sin16°sin44°+cos16°cos44°=cos60°=
;
(7)sin(α+β)cos(γ-β)-cos(β+α)sin(β-γ)=sin(α+β+γ-β)=sin(α+γ);
(8)sin(α-β)sin(β-γ)-cos(α-β)cos(γ-β)=-cos[(α-β)+(β-γ)]=-cos(α-γ);
(9)
=tan(
+
)=tan
=-
;
(10)
=
=tan(β-α).
| 15 |
| 5 |
| 5 |
| π |
| 6 |
(2)
| 3 |
| 2 |
| ||
| 2 |
| 3 |
| π |
| 3 |
(3)
| 3 |
| x |
| 2 |
| x |
| 2 |
| x |
| 2 |
| π |
| 6 |
(4)
| ||
| 4 |
| π |
| 4 |
| ||
| 4 |
| π |
| 4 |
| ||
| 2 |
| π |
| 4 |
| π |
| 3 |
| ||
| 2 |
| 7π |
| 12 |
(5)sin347°cos148°+sin77°cos58°=sin13°cos32°+cos13°sin32°=sin45°=
| ||
| 2 |
(6)sin164°sin224°+sin254°sin314°=-sin16°sin44°+cos16°cos44°=cos60°=
| 1 |
| 2 |
(7)sin(α+β)cos(γ-β)-cos(β+α)sin(β-γ)=sin(α+β+γ-β)=sin(α+γ);
(8)sin(α-β)sin(β-γ)-cos(α-β)cos(γ-β)=-cos[(α-β)+(β-γ)]=-cos(α-γ);
(9)
tan
| ||||
1-tan
|
| π |
| 4 |
| 5π |
| 12 |
| 2π |
| 3 |
| 3 |
(10)
| sin(α+β)-2sinαcosβ |
| 2sinαsinβ+cos(α+β) |
| sin(β-α) |
| cos(β-α) |
点评:本题主要考查了两角和与差的正切函数,两角和与差的正弦函数公式的应用,属于基本知识的考查.

练习册系列答案
相关题目
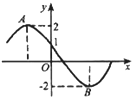 如图所示为函数f(x)=2sin(ωx+φ)(ω>0,
如图所示为函数f(x)=2sin(ωx+φ)(ω>0,| π |
| 2 |
| A、-1 | ||
B、-
| ||
C、
| ||
| D、1 |
若函数y=x•2x 且y′=0,则x=( )
A、-
| ||
B、
| ||
| C、-ln2 | ||
| D、ln2 |
若函数f(x)=-x2+2ax与g(x)=(a+1)1-x在区间[1,2]上都是减函数,则a的取值范围是( )
| A、(-1,0) |
| B、(0,1] |
| C、(0,1) |
| D、(-1,0)∪(0,1] |