题目内容

若函数y=x•2x 且y′=0，则x=（　　）
A、-
1
ln2
B、
1
ln2
C、-ln2
D、ln2
考点：导数的运算
专题：导数的概念及应用
分析：根据导数的基本运算公式即可得到结论．
解答： 解：函数的导数为y′=2x+x•2xln2=2x （1+xln2），
由y′=0得1+xln2=0，解得x=-
1
ln2
，
故选：A
点评：本题主要考查导数的基本计算，要求熟练掌握常见函数的导数公式和导数的运算法则．
练习册系列答案
相关题目
极坐标方程分别为ρ=cosθ与ρ=sinθ的两个圆的圆心距为
 
．
已知函数f（x）=|x|+|2-x|，若g（x）=f（x）-a的零点个数不为0，则a的最小值为
 
．
等比数列{an}的前n项和为Sn，a2=2a1，则
S4
a4
的值是
 
．
已知任意非零实数x，y满足3x2+4xy≤λ（x2+y2）恒成立，则实数λ的最小值是
 
．
若f（x）=
1
log2(x+1)
，则f（x）的定义域为（　　）
A、（-1，0）
B、（-1，+∞）
C、（-1，0）∪（0，+∞）
D、（-∞，-1）
如图所示的程序框图表示求算式“2×4×8×16×32”的值，则判断框内可以填入（　　）
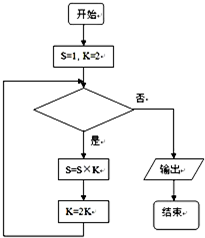
A、k＜10B、k＜20
C、k＜30D、k＜40
化简：
（1）
15
sinx+
5
cosx；
（2）
3
2
cosx-
3
2
sinx；
（3）
3
sin
x
2
+cos
x
2
；
（4）
2
4
sin（
π
4
-x）+
6
4
cos（
π
4
-x）；
（5）sin347°cos148°+sin77°cos58°；
（6）sin164°sin224°+sin254°sin314°；
（7）sin（α+β）cos（γ-β）-cos（β+α）sin（β-γ）；
（8）sin（α-β）sin（β-γ）-cos（α-β）cos（γ-β）；
（9）
tan
5π
4
+tan
5π
12
1-tan
5π
12
；
（10）
sin(α+β)-2sinαcosβ
2sinαsinβ+cos(α+β)
．
已知数列{an}满足a1=1，nan+1=2（n+1）an+n（n+1）．
（1）证明{
an
n
+1}是等比数列，并求{an}的通项公式；
（2）求数列{an}的前n项和Sn．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网