题目内容

A，B是平面α外的两点，它们在平面α内的射影分别是A1，B1，若A1A=3，BB1=5，A1B1=10，那么线段AB的长是
 
．
考点：点、线、面间的距离计算
专题：空间位置关系与距离
分析：画出图形，直接利用解三角形求解线段AB的长即可．
解答： 解：如图：在图1中，过A作AC⊥BB1于C，
由题意可知AC=A1B1=10，BC=2，
∴AB=
AC2+BC2
=
104
=2
26
．
在图2中，过B作BC⊥AA1于C，
由题意可知，AC=3+5=8，BC=A1B1=10，
∴AB=
AC2+BC2
=
82+102
=
164
=2
41
．
所求AB的长为：2
26
或2
41
．
故答案为：2
26
或2
41
．
点评：本题考查空间两点间的距离，注意两种情况，不可漏，是易错题．
练习册系列答案
相关题目
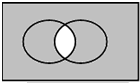
设集合U={1，2，3，4，5}，A={1，3，5}，B={2，3，5}，则图中阴影部分表示的集合是（　　）
A、{1，2，4}B、{4}
C、{3，5}D、∅
设正整数的集合A满足：“若x∈A，则10-x∈A”．
（1）试写出只有一个元素的集合A；
（2）试写出只有两个元素的集合A；
（3）这样的集合A至多有多少个元素？
椭圆有这样的光学性质：从椭圆的一个焦点发出的光线，经椭圆反射后，反射光线经过椭圆的另一个焦点．今有一个水平放置的椭圆形球盘，点A、B是它的两个焦点，长轴长2a=10，焦距2c=6，静放在点A的小球（小球的半径不计）从点A沿直线（不与长轴共线）发出，经椭圆壁反弹后第一次回到点A时，小球经过的路程为
 
．
若等比数列{an}的各项均为正数，且a4a9+a5a8+a6a7=300，则lga1+lga2+…+lga12=
 
．
由下列对象组成的集体，其中为集合的是
 
（填序号）．
①不超过2π的正整数；
②高一数学课本中的所有难题；
③中国的高山；
④平方后等于自身的实数；
⑤高一（2）班中考500分以上的学生．
若双曲线x2-
y2
b2
=1（b＞0）的焦点到其渐近线的距离等于抛物线y2=2px上点M（1，2）到其准线的距离，则实数b=
 
．
曲线y=x3-3x2+1在x=1处的切线方程为（　　）
A、y=3x-4
B、y=-3x+2
C、y=-3x+3
D、y=4x-5
已知函数f（x）=3x3+2x，则f（2）=（　　）
A、10B、28C、31D、18

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网