题目内容
曲线y=x3-3x2+1在x=1处的切线方程为（ ）
| A、y=3x-4 |
| B、y=-3x+2 |
| C、y=-3x+3 |
| D、y=4x-5 |
考点：利用导数研究曲线上某点切线方程
专题：导数的综合应用
分析：求出原函数的导函数，得到x=1时的导数，由直线方程的点斜式得切线方程．
解答：
解：由y=x3-3x2+1，得y′=3x2-6x，
∴y′|x=1=-3．
又当x=1时y=-1．
∴曲线y=x3-3x2+1在x=1处的切线方程为y-（-1）=-3（x-1），
即y=-3x+2．
故选：B．
∴y′|x=1=-3．
又当x=1时y=-1．
∴曲线y=x3-3x2+1在x=1处的切线方程为y-（-1）=-3（x-1），
即y=-3x+2．
故选：B．
点评：本题考查利用导数研究过曲线上某点处的切线方程，过曲线上某点处的切线的斜率，就是函数在该点处的导数值，是中档题．
练习册系列答案
相关题目
由动点P向圆x2-y2=2引两条切线PA，PB，切点分别是A，B．若∠APB=60°，则动点P的轨迹是（ ）
| A、椭圆 | B、圆 | C、双曲线 | D、抛物线 |
设z=3+i，则
等于（ ）
| 1 | ||
|
| A、3+i | ||||
| B、3-i | ||||
C、
| ||||
D、
|
已知c是实数，二次方程x2+x+c=0有两个复数根a，b．若|a-b|=3，则c=（ ）
A、-
| ||
B、
| ||
| C、-2 | ||
| D、2 |
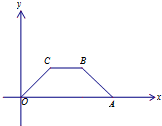如图所示，四边形OABC是上底为1，下底为3，底角为45°的等腰梯形，由斜二测画法，画出这个梯形的直观图O′A′B′C′，在直观图中的梯形的高为（ ）