��Ŀ����
9����֪����${C_1}��\left\{\begin{array}{l}x=1+\frac{{\sqrt{2}}}{2}t\\ y=\frac{{\sqrt{2}}}{2}t\end{array}\right.$��tΪ����������ԭ��Ϊ���㣬��x������Ϊ���ᣬ����������ϵ������${C_2}��\frac{1}{��^2}=\frac{{{{cos}^2}��}}{2}+{sin^2}��$������д������C1����ͨ���̣�����C2��ֱ�����귽�̣�
������M��1��0����������C1������C2����������ͬ�ĵ�A��B����$\frac{|MA|•|MB|}{|AB|}$��ֵ��
���� ������ȥ����t���������C1����ͨ���̣���$\left\{\begin{array}{l}{x=��cos��}\\{y=��sin��}\end{array}\right.$�������������C2��ֱ�����귽�̣�
��������C1��������C2�ķ��̣����A��B�����꣬��������֮��ľ��빫ʽ���������$\frac{|MA|•|MB|}{|AB|}$��ֵ��
��� �⣺����y=$\frac{\sqrt{2}}{2}$t������x=1+$\frac{\sqrt{2}}{2}$t��������x-y-1=0��������C1����ͨ��x-y-1=0��
����${C_2}��\frac{1}{��^2}=\frac{{{{cos}^2}��}}{2}+{sin^2}��$����1=$\frac{{��}^{2}co{s}^{2}��}{2}$+��2sin2�ȣ�
��$\left\{\begin{array}{l}{x=��cos��}\\{y=��sin��}\end{array}\right.$��������C2��ֱ�����귽��$\frac{{x}^{2}}{2}+{y}^{2}=1$��
������$\left\{\begin{array}{l}{y=x-1}\\{\frac{{x}^{2}}{2}+{y}^{2}=1}\end{array}\right.$�������ã�3x2-4x=0����ã�x=0��x=$\frac{4}{3}$��
��A��0��-1����B��$\frac{4}{3}$��$\frac{1}{3}$����
��حMAح=$\sqrt{��1-0��^{2}+��0+1��^{2}}$=$\sqrt{2}$��حMBح=$\sqrt{��\frac{4}{3}-1��^{2}+��\frac{1}{3}-0��^{2}}$=$\frac{\sqrt{2}}{3}$��
��حABح=$\sqrt{��\frac{4}{3}-0��^{2}+��\frac{1}{3}+1��^{2}}$=$\frac{4\sqrt{2}}{3}$��
��$\frac{|MA|•|MB|}{|AB|}$=$\frac{\sqrt{2}��\frac{\sqrt{2}}{3}}{\frac{4\sqrt{2}}{3}}$=$\frac{{\sqrt{2}}}{4}$��
��$\frac{|MA|•|MB|}{|AB|}$��ֵ$\frac{{\sqrt{2}}}{4}$��
���� ���⿼��ֱ�ߵIJ������̣���Բ�ļ����귽�̣�ֱ������Բ��λ�ù�ϵ��������������������е��⣮

 ���ٴ�����ɽ����ϵ�д�
���ٴ�����ɽ����ϵ�д�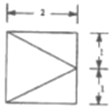 ��֪���������ĵ����DZ߳�Ϊ2�������Σ��丩��ͼ��ͼ��ʾ������ͼΪֱ�������Σ��������������ı�����Ϊ��������
��֪���������ĵ����DZ߳�Ϊ2�������Σ��丩��ͼ��ͼ��ʾ������ͼΪֱ�������Σ��������������ı�����Ϊ��������| A�� | 8�� | B�� | 12�� | C�� | 4�� | D�� | 16�� |
| �������� | ���������� | �ϼ� | |
| ��ѧ���� | 28 | 8 | 36 |
| ��ѧ������ | 16 | 20 | 36 |
| �ϼ� | 44 | 28 | 72 |
��2�����Գ�ȡ������Ƶ��Ϊ���ʣ����ڸ�У�߶�����ѧ���У�����ѧ�����ѧ���������ȡ3�ˣ���XΪ��3�������������������������ѧ������ѧ���������ȡ2�ˣ���YΪ��2����������������������Ǧ�=|X-Y|����εķֲ��м���ѧ������
����x2=$\frac{n��{n}_{11}{n}_{22}-{n}_{21}{n}_{12}��^{2}}{{n}_{1+}{n}_{2+}{n}_{+1}{n}_{+2}}$��
| P��X2��k�� | 0.150 | 0.100 | 0.050 | 0.010 |
| k | 2.072 | 2.706 | 3.841 | 6.635 |