题目内容
下列四个命题:
①在△ABC中,若sinA>sinB,则A>B;
②设△ABC的内角A,B,C所对的边a,b,c成等比数列,则
的取值范围是(
,
);
③Sn为等差数列{an}的前n项和,若a1>0,S6=S9,则S15=-15;
④数列{an}的前n项和为Sn,且满足a1=1,an+1+2Sn=n+1,则S2013=1007;
⑤数列{an}满足a1=33,an+1-an=2n,则
的最小值为
.
其中正确的命题序号 .(注:把你认为正确的序号都填上)
①在△ABC中,若sinA>sinB,则A>B;
②设△ABC的内角A,B,C所对的边a,b,c成等比数列,则
| sinA+cosA•tanC |
| sinB+cosB•tanC |
| ||
| 2 |
| ||
| 2 |
③Sn为等差数列{an}的前n项和,若a1>0,S6=S9,则S15=-15;
④数列{an}的前n项和为Sn,且满足a1=1,an+1+2Sn=n+1,则S2013=1007;
⑤数列{an}满足a1=33,an+1-an=2n,则
| an |
| n |
| 53 |
| 5 |
其中正确的命题序号
考点:命题的真假判断与应用
专题:等差数列与等比数列,解三角形
分析:①借助于正弦定理容易判断;
②由题意b2=ac,再借助于两角和与差公式及正弦定理将后面的式子化简为
,将前式代入任意两边之和大于第三边,构造出
的不等式组解之即可;
③利用性质不难得到a8=0,则s15=0;
④可先推导出通项公式,再求s2013;
⑤先用累加法求出通项公式,再求结果的最小值.
②由题意b2=ac,再借助于两角和与差公式及正弦定理将后面的式子化简为
| b |
| a |
| b |
| a |
③利用性质不难得到a8=0,则s15=0;
④可先推导出通项公式,再求s2013;
⑤先用累加法求出通项公式,再求结果的最小值.
解答:
解:①由正弦定理得
=
,且sinA>sinB,所以上式等价于a>b,根据大边对大角,可得A>B;故①正确;
②由已知得b2=ac,由
=
=
=
=
=
;不妨令
=t>0,
将c=
代入a+b>c,后得a2+ab>b2,两边同除以a2结合t=
得t2-t-1<0,解得
<t<
①,
同理将c=
分别带入a+c>b,b+c>a整理化简后解得t<
或t>
,联立①式解得
<t<
,故②正确;
③由s6=s9得a7+a8+a9=3a8=0,所以s15=
=15a8=0,故③错;
④由an+1+2Sn=n+1得 an+2sn-1=n,两式相减得an+1+an=1,又a2+2a1=2,所以a2=0,该数列为1,0,1,0,1,0…,即偶数项为0,奇数项为1,所以s2013=
+1=1007.故④正确;
⑤利用累加法可得an-a1=2×(1+2+3+…+(n-1))=n(n-1),故an=33+n(n-1),∴
=
=n+
-1,由于函数y=x+
在(0,
)递减,在[
,+∞)上递增,结合n∈N*,易知n=6时,
最小值为
,故⑤错.
故答案为①②④
| a |
| sinA |
| b |
| sinB |
②由已知得b2=ac,由
| sinA+cosA•tanC |
| sinB+cosB•tanC |
sinA+cosA
| ||
sinB+cosB
|
| sinAcosC+cosAsinC |
| sinBcosC+cosBsinC |
| sin(A+C) |
| sin(B+C) |
| sinB |
| sinA |
| b |
| a |
| b |
| a |
将c=
| b2 |
| a |
| b |
| a |
1-
| ||
| 2 |
1+
| ||
| 2 |
同理将c=
| b2 |
| a |
-1-
| ||
| 2 |
-1+
| ||
| 2 |
-1+
| ||
| 2 |
1+
| ||
| 2 |
③由s6=s9得a7+a8+a9=3a8=0,所以s15=
| 15(a1+a15) |
| 2 |
④由an+1+2Sn=n+1得 an+2sn-1=n,两式相减得an+1+an=1,又a2+2a1=2,所以a2=0,该数列为1,0,1,0,1,0…,即偶数项为0,奇数项为1,所以s2013=
| 2012 |
| 2 |
⑤利用累加法可得an-a1=2×(1+2+3+…+(n-1))=n(n-1),故an=33+n(n-1),∴
| an |
| n |
| n2-n+33 |
| n |
| 33 |
| n |
| 33 |
| x |
| 33 |
| 33 |
| an |
| n |
| 21 |
| 2 |
故答案为①②④
点评:这是一道有关推理的问题,主要是考查了等差数列、数列求和、解三角形有关基础知识,思维量较大,做题时需仔细认真方能少出错.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
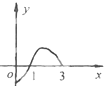 定义在(0,3)上的函数f(x)的图象如图所示
定义在(0,3)上的函数f(x)的图象如图所示