题目内容
抛物线y2=-x上的点P到直线4x+3y-8=0的距离的最小值为 和此时点P的坐标为 .
考点:直线与圆锥曲线的关系
专题:圆锥曲线的定义、性质与方程
分析:设P(x,y)为该抛物线上任一点,利用点到直线间的距离公式可求得点P到直线x+y+4=0的距离d的关系式,即可求得dmin.然后求出坐标.
解答:
解:设P(x,y)为该抛物线上任一点,那么y2=-x,
则点P到直线4x+3y-8=0的距离d=
=
=
≥
,
当且仅当y=
时,取“=”.
此时点P(-
,
).
即抛物线上的点P的坐标为P(-
,
)时,点P到直线x+y+4=0的距离最短,最小值为
.
故答案为:
;P(-
,
).
则点P到直线4x+3y-8=0的距离d=
| |4x+3y-8| | ||
|
| |-4y2+3y-8| |
| 5 |
|4(y-
| ||||
| 5 |
| 119 |
| 80 |
当且仅当y=
| 3 |
| 8 |
此时点P(-
| 9 |
| 64 |
| 3 |
| 8 |
即抛物线上的点P的坐标为P(-
| 9 |
| 64 |
| 3 |
| 8 |
| 119 |
| 80 |
故答案为:
| 119 |
| 80 |
| 9 |
| 64 |
| 3 |
| 8 |
点评:本题考查抛物线的简单性质,考查点到直线间的距离公式与两点间的距离公式,属于中档题.

练习册系列答案
相关题目
对?k∈R,则方程x2+ky2=1所表示的曲线不可能是( )
| A、两条直线 | B、圆 |
| C、椭圆或双曲线 | D、抛物线 |
已知圆锥的母线长为5cm,圆锥的侧面展开图如图所示,且∠AOA1=120°,一只蚂蚁欲从圆锥的底面上的点A出发,沿圆锥侧面爬行一周回到点A.则蚂蚁爬行的最短路程长为( ) 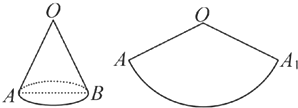

| A、8 cm | ||
B、5
| ||
| C、10 cm | ||
| D、5πcm |