已知圆锥的母线长为5cm.圆锥的侧面展开图如图所示.且∠AOA1=120°.一只蚂蚁欲从圆锥的底面上的点A出发.沿圆锥侧面爬行一周回到点A．则蚂蚁爬行的最短路程长为( ) A.8 cmB.53cmC.10 cmD.5πcm 题目和参考答案——青夏教育精英家教网—

题目内容

已知圆锥的母线长为5cm，圆锥的侧面展开图如图所示，且∠AOA₁=120°，一只蚂蚁欲从圆锥的底面上的点A出发，沿圆锥侧面爬行一周回到点A．则蚂蚁爬行的最短路程长为（　　）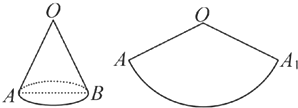

A、8 cm

B、5

C、10 cm

D、5πcm

考点：多面体和旋转体表面上的最短距离问题

专题：计算题,空间位置关系与距离

分析：圆锥的底面周长也就是圆锥的侧面展开图的弧长，利用弧长公式即可求得侧面展开图的圆心角，进而构造直角三角形求得相应线段即可．

解答： 解：连接AA′，作OC⊥AA′于C，

∵圆锥的母线长为5cm，∠AOA₁=120°，
∴AC=

∴AA′=2AC=5

．
故选B．

点评：本题考查了圆锥的计算，求立体图形中两点之间的最短路线长，一般应放在平面内，构造直角三角形，求两点之间的线段的长度．用到的知识点为：圆锥的弧长等于底面周长．

练习册系列答案

相关题目

，k∈Z}，B={x|x²≤36}，试求A∩B．

在三角形ABC中，角A，B，C所对的边a，b，c，若a=

，b=

，asinBcosC+csinBcosA=

，则角A

．

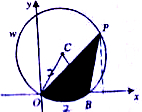如图，在平面直角坐标系xOy中，⊙C经过点O，交x轴正半轴于点B（2，0），P是弧OwB上的一个动点，且∠OPB=30°，设P点坐标为（m，n）．
（1）当n=2

，求m的值；
（2）设图中阴影部分的面积为S，求S与n之间的函数关系式，并求S的最大值；
（3）试探索动点P在运动过程中，是否存在整点P（m，n）（横、纵坐标都为整数的点叫整点）？若存在，请求出，若不存在，请说明理由．

抛物线y²=-x上的点P到直线4x+3y-8=0的距离的最小值为

（1）已知两圆x²+y²-10x-10y=0，x²+y²+6x-2y-40=0，求它们的公共弦所在直线的方程；
（2）已知圆M：x²+（y-2）²=1，Q是x轴上的动点，QA，QB分别切圆M于A，B两点，求动弦AB的中点P的轨迹方程．

已知等比数列{a_n}的前n项和为S_n，a₁=1，且S₂+

a₂=4．
（1）求数列{a_n}的通项公式；
（2）记b_n=a_n•log₂a_n，求数列{b_n}的前n项和T_n．

试题分类