题目内容
函数y=x-lnx，x∈（0，1]的值域是 ．
考点：利用导数求闭区间上函数的最值,函数的值域
专题：导数的概念及应用
分析：由题意得f′（x）分析得到函数f（x）=x-lnx在（0，1]上是减函数，
所以当x=1时函数f（x）有最小值1，当x趋向于0时函数值趋向于+∞．
所以当x=1时函数f（x）有最小值1，当x趋向于0时函数值趋向于+∞．
解答：
解：∵函数y=x-lnx，x∈（0，1]
∴y′=1-
=
，x∈（0，1]，
即x∈（0，1]，y′≤0，
∴函数y=x-lnx，x∈（0，1]单调递减，
x=1，y=1-0=1，
当x趋向于0时函数值趋向于+∞．
所以函数f（x）=x-lnx在（0，1]上的值域为[1，+∞）．
故答案为：[1，+∞）．
∴y′=1-
| 1 |
| x |
| x-1 |
| x |
即x∈（0，1]，y′≤0，
∴函数y=x-lnx，x∈（0，1]单调递减，
x=1，y=1-0=1，
当x趋向于0时函数值趋向于+∞．
所以函数f（x）=x-lnx在（0，1]上的值域为[1，+∞）．
故答案为：[1，+∞）．
点评：解决此类问题关键是正确求函数的导数并且分析导数的符号判断出原函数的单调性，进而求出函数的最值得出函数的值域．属于中档题．
练习册系列答案
小学学习好帮手系列答案
小学同步三练核心密卷系列答案
相关题目
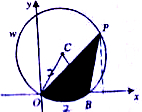如图，在平面直角坐标系xOy中，⊙C经过点O，交x轴正半轴于点B（2，0），P是弧OwB上的一个动点，且∠OPB=30°，设P点坐标为（m，n）．在数列{an}中，anan+1=
，a1=1，则a98+a101=（ ）
| 1 |
| 2 |
| A、6 | ||
| B、1 | ||
| C、2 | ||
D、
|