题目内容
若不等式ax2>lnx+1对任意x∈(0,+∞)恒成立,求实数a的取值范围.
考点:函数恒成立问题
专题:函数的性质及应用,导数的综合应用
分析:先分离参数,化为a>
,在x∈(0,+∞)上恒成立,然后只需求出f(x)=
,(x>0)的最大值即可.结合导数的知识容易解决问题.
| lnx+1 |
| x2 |
| lnx+1 |
| x2 |
解答:
解:若不等式ax2>lnx+1对任意x∈(0,+∞)恒成立,
只需a>
,在x∈(0,+∞)上恒成立,
令f(x)=
,(x>0)
因为f′(x)=-
,(x>0),
令f′(x)=0得x=
,易知当x∈(0,
)时,f′(x)>0;当x∈(
,+∞)时,f′(x)<0.
故f(x)在(0,
]上递增,在(
,+∞)上递减.
所以f(x)max=f(
)=
.
故要使原不等式恒成立,只需a>
,
即所求a的范围是(
,+∞).
只需a>
| lnx+1 |
| x2 |
令f(x)=
| lnx+1 |
| x2 |
因为f′(x)=-
| 2lnx+1 |
| x3 |
令f′(x)=0得x=
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
故f(x)在(0,
| 1 | ||
|
| 1 | ||
|
所以f(x)max=f(
| 1 | ||
|
| e |
| 2 |
故要使原不等式恒成立,只需a>
| e |
| 2 |
即所求a的范围是(
| e |
| 2 |
点评:本题考查了不等式恒成立问题的基本思路,一般是转化为函数的最值问题求解,能分离参数的尽量分离参数,注意导数在研究函数最值问题中的应用.

练习册系列答案
相关题目
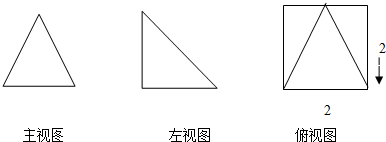
若空间几何体的三视图如图所示,则该几何体体积为( )

A、
| ||||
B、
| ||||
C、
| ||||
| D、8 |
点P为底边长为2
,高为2的正三棱柱表面上的动点,MN是该棱柱内切球的一条直径,则
•
取值范围是( )
| 3 |
| PM |
| PN |
| A、[0,2] |
| B、[0,3] |
| C、[0,4] |
| D、[-2,2] |