题目内容
在?ABCD中，AB=2，AD=1，∠DAB=60°，F为DC的中点，E为线段BC上的一个点，若
•
=
，则
•
= ．
| AE |
| AF |
| 15 |
| 4 |
| AE |
| AB |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：由已知设
=λ
，利用在?ABCD中，AB=2，AD=1，∠DAB=60°，F为DC的中点，将等式化为λ的方程解之；然后将所求化为平行四边形的边表示的数量积展开求值．
| BE |
| BC |
解答：
解：由已知设
=λ
，因为在?ABCD中，AB=2，AD=1，∠DAB=60°，F为DC的中点，
所以
•
=（
+
）（
+
）=
•
+
•
+
•
+
•
=2×1×
+2×2×
+λ+
×2λ×
=
，
解得λ=
，
所以
•
=（
+
）•
=
2+
•
=4+
×1×2×cos60°=4
．
故答案为：4
．
| BE |
| BC |
所以
| AE |
| AF |
| AB |
| BE |
| AD |
| DF |
| AB |
| AD |
| AB |
| DF |
| BE |
| AD |
| BE |
| DF |
=2×1×
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 15 |
| 4 |
解得λ=
| 1 |
| 2 |
所以
| AE |
| AB |
| AB |
| 1 |
| 2 |
| BC |
| AB |
| AB |
| 1 |
| 2 |
| BC |
| AB |
| 1 |
| 2 |
| 1 |
| 2 |
故答案为：4
| 1 |
| 2 |
点评：本题考查了向量的数量积以及向量的三角形法则的运用；需要注意向量的夹角．
练习册系列答案
作业辅导系列答案
同步学典一课多练系列答案
经典密卷系列答案
相关题目
已知f（x）=
，则
的值是（ ）
| x |
| lim |
| △x→0 |
| f(x-△x)-f(x) |
| △x |
A、-
| ||||
B、
| ||||
C、-
|
设两个命题p、q，其中p：?x∈R，不等式x2+2x-1＞0恒成立；q：当
＜a＜1时，函数f（x）=（4a-3）x在R上为减函数，则下列命题为真命题的是（ ）
| 3 |
| 4 |
| A、p∧q | B、￢p∧￢q |
| C、￢p∧q | D、p∧￢q |
若
=（sin2x，cos2x），
=（sin2x，-cos2x），f（x）=
•
+4cos2x+2
sinxcosx．如果?m∈R，对?x∈R都有f（x）≥f（m），则f（m）等于（ ）
| a |
| b |
| a |
| b |
| 3 |
A、2+2
| ||
| B、3 | ||
| C、0 | ||
D、2-2
|
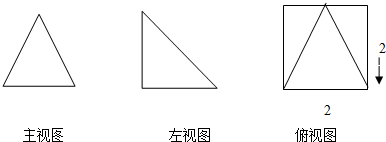
若空间几何体的三视图如图所示，则该几何体体积为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
| D、8 |