题目内容

在△ABC中，AC=1，AB=2，∠A的平分线AD=
6
2
，则BC=
 
．
考点：三角形中的几何计算
专题：解三角形
分析：根据角平线的性质，可设AD=2x，CD=x，然后结合余弦定理列方程解之即可．
解答： 解：因为AD是∠A的平分线，所以
AB
AC
=
BD
CD
，
不妨设AD=2x，CD=x，
结合已知得cos∠BAD=cos∠CAD，
由余弦定理得
22+(
6
2
)2-(2x)2
2×
6
2
×2
=
1+(
6
2
)2-x2
2×1×
6
2
，
解得x=±
1
2
，负值舍去，故x=
1
2
，所以BC=3x=
3
2
．
故答案为
3
2
点评：本题考查了解三角形的有关知识和方法，解题的关键是角平分线的性质以及利用两个角相等结合余弦定理列出方程求解．
练习册系列答案
相关题目
若点P在-
10π
3
角的终边上，且P的坐标为（-1，y），则y等于（　　）
A、-
3
3
B、
3
3
C、-
3
D、
3
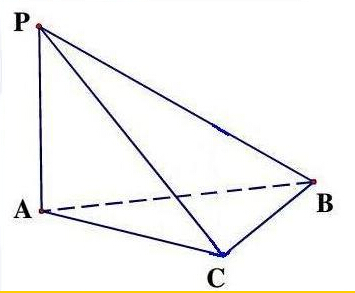如图所示，在四面体P-ABC中，已知PA=BC=6，PC=AB=10，AC=8，PB=2
34
，求证：BC⊥平面PAC，PA⊥平面ABC．
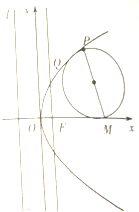如图，设F为抛物线y2=2px（p＞0）的焦点，P是抛物线上一点，Q为线段OF的垂直平分线上一点，且点Q到抛物线的准线l的距离为
3
2
．
（1）求抛物线的方程；
（2）设点M的坐标为（3，0），是否垂直于x轴的直线l′被以PM为直径的圆截得的弦长为定值？若存在，求直线l′的方程；若不存在，请说明理由．
下列命题正确的是（　　）
①平行于同一平面的两直线平行；
②垂直于同一平面的两直线平行；
③平行于同一直线的两平面平行；
④垂直于同一直线的两平面平行．
A、①②B、③④C、①③D、②④
已知三个数成等比数列，他们的乘积是216，若把第三个数减去8，就成等差数列，求这三个数．
过抛物线y2=ax 的焦点作直线交抛物线于A（x1，y1），B（x2，y2）两点，如果x1+x2=8且|AB|=10，则a=
 
．
已知曲线C的极坐标方程是ρ=4cosθ．以极点为平面直角坐标系的原点，极轴为x轴的正半轴，建立平面直角坐标系，直l的参数方程是
x=1+tcosα
y=tsinα
（t是参数）
（1）将曲线C的极坐标方程化为直角坐标方程；
（2）若直线l与曲线C相交于A、B两点，且|AB|=
14
，求直线的倾斜角α的值．
若不等式sin2x+2acosx≤a2+3a-2（a＜0）对一切x∈R恒成立，则实数a的最大值是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网